В
раздел «Клиодинамика и Синергетика»
Серия «Синергетика»
Научно-исследовательский центр
«Синергетика»
Санкт-Петербургского союза учёных
СИНЕРГЕТИКА
ВСЕЛЕННАЯ
РЕЗОНАНСОВ
Г. И. Басина, М. А. Басин
Работа выполнена при поддержке:
РФФИ (гранты №95-01-1582а, №96-06-80418а,
№00-06-80077а);
РГНФ (гранты №00-03-36003а/Б,
№03-03-00247а/Б, № 07-03-90309а/Б)
В монографии приводятся некоторые
общепринятые определения понятия «резонанс». Рассмотрены различные типы
математических моделей, описывающих резонансные взаимодействия. Приведены примеры резонансных процессов в различных
природных явлениях и областях техники.
Разработана
новая классификация волновых движений сплошной среды, вихревых, грибовидных
(дипольных) и древовидных структур, а также транспортно информационных систем.
Определены условия проявления волновых
резонансов.
Изложены
основные идеи теории и изучены экспериментальные проявления вновь открытого
явления:- вихре - волнового и
структурного резонанса. Определены необходимые условия возникновения и
существования и осуществлена классификация резонансов нового типа. Предсказана
возможность проявления открытого явления в различных природных и социальных
процессах.
Высказано
предположение, что эволюция транспортно-информационных систем, в том числе,
появление и развитие контроллера , может рассматриваться как цепочка
бифуркационных событий, связанных с последовательно развивающимися структурными
резонансами между структурой, полем и контроллером.
Предисловие
Настоящее
издание продолжает серию монографий под общим названием «Синергетика»,
издаваемых Научно-исследовательским центром «Синергетика» Санкт- Петербургского
союза учёных и издательством «Норма» - Санкт-Петербург.
В
книге представлен краткий обзор природных явлений и соответствующих им математических
моделей, которые могут быть объединены одним словом: «резонанс». Выполнен
предварительный лингвистический анализ этого слова, в том числе и путём его
перевода с русского на другие европейские языки.
Анализ
частоты встречаемости слова «резонанс» в поисковых системах сети Internet
показал его
чрезвычайную популярность не только среди учёных, стремящихся облечь содержание
этого слова в чёткие математические формулы, но и среди людей различных
профессий, в том числе и бизнесменов, включающих слово «резонанс» и его
производные в названия своих фирм и проектов.
Показано
также, что математическая модель, которая была предложена для описания
классического резонанса, стала жить собственной жизнью. Развиваясь и
усложняясь, математические построения позволяют открыть «на кончике пера», а
затем обнаружить в реальных условиях новые явления, которые также могут быть
названы резонансными. Особенно бурное развитие этих процессов происходило в
70-90 годах прошлого века, когда всерьёз начались исследования нелинейных
волновых процессов и возникла Cинергетика - наука о самоорганизации сложных
структур и систем. Исследования всё новых типов резонансов, приводящих к
хаотизации процессов и (или) самоорганизации новых структур стали существенной
составляющей синергетических исследований. «Вселенная резонансов» стала частью
Синергетики.
Этот
синтез позволил обнаружить среди большого разнообразия сценариев
формирования структур новый резонансный
сценарий, названный «вихре - волновым или структурным резонансом». Удалось
построить безразмерный критерий, равенство которого единице является
необходимым условием возникновения волновых резонансов нового типа.
Стимулировать
читателя к поиску и обнаружению в различных природных и социальных явлениях
резонансных процессов нового типа и их детальному исследованию и использованию
- цель настоящей монографии.
SYNERGETICS
UNIVERSE
OF RESONANCES
Galina
I. Basina
Scientific
199034. St.-Petersburg.
Tel. №
+7 (812)3284124. Fax №:+7(812)3284124:
E-mail:.
basin@yandex.ru
The work was
supported by:
The Russian
Foundation of Basic Research
(Grants №№95-01-1582a, 96-06-80418a, 00-06-80077а).
The Russian
Humanitarian Foundation
(Grants №№00-03-36003а/Б, 03-03-00247а/Б, 07-03-90309 а/Б).
Abstract
This book represents the information about different
manifestations of one of unusual phenomena, which is meeting in natural and in
social systems – resonance interaction. The linguistic analysis of the word:
„resonance“ - was worked out. The field of words in European languages, which
are related with this world, is found. Determinations of conception
“resonance”, given by different authors, are presented.
The connection between the usual representation about
resonance at the perception and intensification of the sound and at the
analysis of many other physically phenomena, and mathematically model, allowed
to the scientists to give the sufficiently strange determination to the
conception of the oscillatory resonance.
However, the
mathematically model of oscillatory resonance turned to be capable to live for
his laws, complicating and developing. New forms of dynamically models
generated new conceptions about resonance interactions. So appeared the ideas
of inner resonances in dynamically systems, parametric resonances in systems of
differential equations with variable coefficients.
A number of new forms of resonance phenomena was
discovered at the analysis of the nonlinear equations. Essentially must be
distinguished the problem of interaction between the resonance and self-
oscillating regimes. At their interaction occur new phenomena, such as
stochastic regimes, determined chaos, synchronization and competition of
oscillations (modes). The change of variables and complexification of usually
differentially equations also widens representations about possible forms of
resonance phenomena.
Theoretically
analysis of mathematically models of chains of oscillators and wave phenomena
allowed turn to study of resonances, arising in the continuous medium. Their
specific concludes in the fact that may come in resonance the parameters of the
system, depending not from time, but from space coordinates. Resonance may be
not only frequencies but also velocities and lengths of the waves. At the same
time the factors, acting on the arising of the resonances in the oscillating
systems (nonlinearity, dependence of the parameters of the equations from the
time) continue to act on the system.
The
phenomena, connected with arising of waves and vortex systems of different nature,
are widely studying in the mechanics of continuous medium. Their sources in
many cases are the driving in the continuous medium hard or flexible bodies. In
the inhomogeneous media may appear dispersing waves, which velocity of motion
depends from their length. At the interaction of driving bodies with fluid or
gas in these media may occur phase transitions and appear new vortex and
mushroom (dipole) structures and boundary divisions (for example, cavitation,
condensation of vapor, crystallization).
Classification of nonlinear waves, structures and
systems and working out of new
mathematically models allowed to discover
new phenomenon:
“Vortex – wave and structural resonance”.
The essence
of this phenomenon consists in resonant non-linear interplay between dispersing
waves and demarcations of environments (particularly, vapor and air cavities),
arising in continuum, and vortex and mushroom patterns, forming in the medium
near the boundaries of driving bodies.
Resonance
interaction results in qualitative changes of characteristics of interacting
objects, formation of new vortex - wave patterns and abnormal change of the
forces, acting on the body.
Particularities
of nonlinear resonance interaction appear most clear by the existence of angle
points on the boundaries of the bodies, near which form new vortex and mushroom
structures.
Characteristic
example of vortex-wave and structural resonance is the regime of flow, arising near
the hydrofoil, driving near the free surface of heavy liquid in the region of
Froude numbers .( , where -velocity of relative motion of the body
(hydrofoil) and liquid, - gravity
acceleration, -hydrofoils chord) and
relative depths of submersion and by
for .
There were discovered theoretically and
experimentally anomalous changes of hydrodynamic forces, acting on the body,
and forming of complex vortex-wave and mushroom structures.
Theoretically
analysis of the particularities of the vortex-wave and structural resonance at
the motion of the body in stratificated liquid or gas allowed predict the
relations between gradients of density, Froude numbers and relative depths,
corresponding to the appearance of this anomalous flow regime.
It was
discovered, that by the decreasing of the degree of non-homogeneity of liquid
or gas the intensity of flow disturbances, corresponding to the vortex-wave and
structural resonance, change small, but the region of resonance meanings of
Froude numbers narrows, and their meanings tend to zero.
So, even by
small degree of non-homogeneity of the medium and small relative velocities of
bodies motion in consequence of the
resonance interaction the driving lifting body may stimulate in liquid (gas)
medium significant concentrated vortex-wave disturbances, bringing to
appearance of new resonance structures in the flow.
The detail
investigation of these resonance phenomena and comparison of theoretically and
experimentally data leaded to the creation of principally new classification of
wave and vortex motions and to the creation of general conception of
vortex-wave and structural resonance.
We
succeeded in explaining as specifically form of vortex- wave and structural
resonance also and transitional regime of cavitating flow near the hydrofoil,
when the length of the cavity is near to its chord.
Analogous
nonlinear resonance phenomena were observed also by the investigation of
interaction of cavitating hydrofoils, by the non-stationary flow of bluff
bodies, by the interaction of two and more hydrofoils, by the motion of the
wing near the solid boundary and so on.
Common for all investigated
phenomena is the wave character of deformations of non-homogeneous medium,
existence of resonance interaction between circulation flows near the bodies
and wave motions in the media and the forming of new nonlinear resonance
vortex-wave structures. This fact allowed us to consider these processes as
different forms of manifestation of unknown earlier physically phenomena – vortex-wave
and structural resonance. The main conditions of such resonance phenomena
arising are determined.
Fulfilled
theoretically and experimentally investigations opened wide perspectives in the
investigation of new forms of vortex-wave and structural resonance by the
motion of the bodies in the multivendor atmosphere and plasma, at the
investigation of biologically, social and ecologically systems, and also by the
investigation of interaction of discovered vortex-wave resonance structures
with another types of oscillating, wave and vortex motions, particularly, with
oscillations of solid bodies in the liquid and vibrations of elastic
constructions.
Содержание
1.Введение.
Глава I. Резонансы
в конечномерных динамических системах.
1.Классические определения
резонанса.
2. Первичный
лингвистический анализ слова «резонанс».
3. Исследование
частоты встречи слова резонанс в Internet.
4. Смысл,
вкладываемый в это слово различными авторами.
5. Простейшее
математическое уравнение, решение которого даёт представление о классическом
резонансе..
6. Внутренние
резонансы в системах линейных дифференциальных уравнений с конечным числом
степеней свободы.
7. Параметрический
резонанс.
8. Нелинейные резонансы
в динамических системах. Влияние нелинейности на тип резонансной кривой.
Основные соотношения между возмущающей частотой и резонансными частотами.
9. Нелинейные
резонансы и автоколебания.
10.Резонансы в
системах, описываемых комплексными уравнениями.
11. Резонансные
явления при произвольных внешних воздействиях.
12. О возможности
степенных резонансов.
Глава II. Волны и
волновые резонансы.
1. Анализ
одномерного линейного волнового уравнения .
2. Классификация
нелинейных волн, структур и систем.
3. Умеренно
нелинейные волны.
Глава III. Вихревые
и грибовидные структуры. Транспортно-информационные системы.
1. Вихревые ударные волны первого рода.
Формирование вихревых пузырей. Ревербераторы.
2. Вихревые ударные волны второго рода.
Вихревые пелены.
3. Грибовидные структуры .
4. Возможные формы качественной трансформации
грибовидных структур. Древовидные структуры.
5. Транспортно-информационные системы.
Глава IV Вихре-
волновой и структурный резонанс. История открытия
1. Результаты теоретических и экспериментальных
исследований сил действующих на тела, движущиеся в ограниченном водоёме.
Обнаружение критических значений чисел Фруда по длине тела и глубине жидкости.
2. Теоретические и экспериментальные
исследования движения крыла вблизи экрана. Аномальное увеличение
гидро-аэродинамического качества крыла при приближении к экрану. Математическое
моделирование . Метод сращиваемых разложений. Квадрупольная теория. Аналогия с
формированием грибовидных структур.
3. Кавитационное обтекание крыла. Аномалии
переходного режима. Результаты
теоретических и экспериментальных исследований.
4. Нелинейные резонансы поверхностных и
внутренних волн. Эволюция идеи.
5. Движение крыла вблизи границы раздела сред.
Аномальный режим обтекания. Результаты теоретических и экспериментальных
исследований.
6. Рождение концепции вихре -волнового и
структурного резонанса.
Глава V.
Вихре-волновой и структурный резонанс. Концепция работает.
1. Основные
волновые параметры движущегося тела как уединённой волны.
2. Классификация
вихре - волновых и структурных резонансов..
3а.
Пространственные резонансы - аналогия с симметриями.
3. Резонанс по
скорости.
4. Дисперсионные
свойства сплошной среды.
5. Движение тела на
мелководье.
6. Околозвуковое и
сверхзвуковое движение тел.
7. Структурно вихревой резонанс по скорости и
продольному размеру.
8. Основной
безразмерный параметр вихре - волнового и структурного резонанса.
9. Горб волнового
сопротивления тел в ограниченном фарватере как результат резонансного
взаимодействия второго класса.
10. Вихре -
волновой резонанс при движении крыла вблизи границы раздела сред . Численный и
качественный анализ. Сопоставление теории с экспериментальными данными.
11. Вихре –
волновой резонанс в стратифицированной сплошной среде. Теоретические
предсказания. Необходима экспериментальная проверка полученного результата.
12. Резонансы в
неоднородной среде. Предсказание условий возниковения резонансных явлений.
13. Вихре волновой
и структурный резонанс в магнитной гидродинамике. Качественные предсказания.
14. Движение крыла
вблизи экрана как проявление четвёртой формы вихре – волнового резонанса.
Биологические и технические приложения.
15. Переходный
режим кавитации как проявление одной из форм четвёртого класса –
структурно-вихревого резонанса.
16. О возможности
обнаружения новых форм вихре-волнового и структурного резонанса в биологических
и социальных явлениях.
Заключение
Введение
«…Совместное
рассмотрение различных видов пространственных и временных резонансных явлений в
рамках синергетики может привести к дальнейшему прогрессу в понимании
закономерностей организации объектов живой и неживой природы».
А. Ю.
Сунгуров [1].
«Изучая
процессы самоорганизации в творческом акте переживания, человек вовлекается в соответствующее
движение мысли и тем самым развивается сам. В целостном общении возникает
синдром Пигмалиона. Создавая Галатею
синергетики, мы попадаем под её обаяние, способствующее сотрудничеству,
сочувствию, соединению».
Р. Г.
Баранцев [2].
«… при определённой
амплитуде инноваций существует опасность, что резонирующая инновация станет
причиной деградации системы»
Н. В. Басов
[3]
В настоящей
монографии представлена краткая информация о различных проявлениях одного из необычных
явлений, встречающегося в природных и социальных системах, - резонансного
взаимодействия. Произведён краткий лингвистический анализ слова «резонанс».
Найдено поле слов и терминов в европейских языках, родственных этому слову.
Приводятся определения понятия «резонанс», данные различными авторами.
Связь между обыденным представлением о
резонансе при восприятии и усилении звука и анализе многих других физических
явлений, и математической моделью, позволила учёным дать достаточно строгое
определение понятию колебательного резонанса. Однако, математическая модель
колебательного резонанса оказалась способной жить по своим законам, усложняясь
и развиваясь. Новые формы динамических моделей породили новые представления о
резонансных взаимодействиях. Так появились понятия внутренних резонансов в динамических
системах, параметрических резонансов в системах дифференциальных уравнений с
переменными коэффициентами.
Ряд новых форм резонансных явлений
обнаружен при анализе нелинейных дифференциальных уравнений. Особо следует
выделить проблему взаимодействия резонансных и автоколебательных процессов. При
этом возникают новые явления, такие, как стохастизация, детерминированный хаос,
синхронизация и конкуренция колебаний (мод).
Замена переменных и
комплексификация обыкновенных дифференциальных уравнений также расширяют
представления о возможных моделях резонансных явлений
Теоретический анализ математических
моделей цепочек осцилляторов и волновых явлений позволил перейти к изучению
резонансов, возникающих в сплошной среде. Их специфика заключается в том, что
резонируют параметры системы, зависящие не только от времени, но и от
пространственных координат. Резонансными могут стать не только частоты, но и
скорости и длины волн. При этом факторы, влияющие на возникновение резонансов в
колебательных системах (нелинейность, зависимость параметров уравнений от
времени), продолжают действовать.
Явления, связанные с возникновением волн и
вихревых структур различной природы, широко изучаются в механике сплошных сред.
Их источниками во многих случаях являются движущиеся в сплошной среде жесткие
или деформируемые тела. В неоднородных средах могут возникать диспергирующие
волны, скорость перемещения которых зависит от их длины. При взаимодействии
движущихся тел с жидкостью или газом в этих средах могут происходить фазовые
переходы и возникать новые вихревые и грибовидные (дипольные) структуры и
границы раздела сред (например, кавитация, конденсация паров, кристаллизация).
Классификация
нелинейных волн, структур и систем и разработка новых математических моделей
позволили открыть новое явление
- Вихре - волновой
и структурный резонанс.
Сущность этого явления состоит в нелинейном
взаимодействии волн и границ раздела сред (в частности, паровых и воздушных
каверн), возникающих в сплошной среде, и вихревых и грибовидных структур,
формирующихся вблизи границ движущихся объектов. Резонансное взаимодействие
приводит к качественному изменению характеристик взаимодействующих объектов,
формированию новых вихре - волновых структур и аномальному изменению сил,
действующих на движущееся тело. Специфика нелинейного резонансного
взаимодействия наиболее ярко проявляется при наличии у границ тел угловых
точек, вблизи которых формируются новые вихревые структуры.
Характерным
примером вихре – волнового и структурного резонанса является режим течения,
возникающий около крыла, движущегося вблизи свободной поверхности весомой
жидкости в определённом диапазоне чисел Фруда
(где - скорость относительного
движения тела (крыла) и жидкости, -
ускорение силы тяжести, -хорда крыла) и
относительных глубин погружения. В этом режиме теоретически и экспериментально
исследованы аномальные изменения гидродинамических сил, действующих на тело, а
также обнаружено формирование новых вихре – волновых и грибовидных структур.
Теоретический
анализ особенностей вихре - волнового и структурного резонанса при движении
тела в стратифицированной жидкости или газе позволил предсказать соотношения
между градиентами плотности, числами Фруда и относительными погружениями, при которых
возможно наступление вихре - волнового и структурного резонанса. Было
обнаружено, что при уменьшении степени неоднородности жидкости интенсивность
возмущений потока, сопровождающих вихре – волновой и структурный резонанс,
ослабевает незначительно, однако зона резонансных величин чисел Фруда сужается,
а их значения стремятся к нулю.
Таким образом, даже
при малой степени неоднородности среды и небольших относительных скоростях
движения тела вследствие обнаруженного резонансного взаимодействия движущееся
несущее тело может вызывать в жидкой (газообразной) среде значительные
концентрированные возмущения.
Удалось объяснить
как специфическую форму вихре – волнового и структурного резонанса также и
переходный режим кавитационного обтекания крыла, когда длина паровой или
газовой каверны близка к его хорде.
Аналогичные по
характеру нелинейные явления были обнаружены также при взаимодействии
кавитирующих крыльев, при нестационарном обтекании плохообтекаемых тел, при
аэродинамическом взаимодействии двух или нескольких крыльев, при движении крыла
вблизи экрана, при движении тел в сжимаемой среде и на мелководье.
Общим для всех
вновь обнаруженных и исследованных течений является волновой характер
деформаций неоднородной среды,
существование резонансного взаимодействия между вихревыми течениями около тел и волновыми движениями в
неоднородной среде, а также формирование новых нелинейных резонансных вихре -
волновых структур.
Введён в
рассмотрение новый безразмерный параметр, равенство которого единице определяет
необходимое условие существования вихре-волнового и структурного резонанса.
Выполненные
теоретические и экспериментальные исследования открыли широкие перспективы в
изучении новых форм вихре - волнового и структурного резонанса в изучении
биологических, социальных и экологических систем, а также в исследовании
взаимодействия уже открытых вихре - волновых резонансных структур с другими
видами колебательных, волновых и вихревых движений, в частности, с колебаниями
твердых тел в жидкости, вибрациями упругих конструкций.
Глава I.
Резонансы в конечномерных динамических системах.
1.
Классические определения резонанса.
Важным
элементом синергетической методологии изучения того или иного объекта является
лингвистический анализ слова, которым он обозначен, и поиск определений,
даваемых этому объекту различными авторами [4].
Ниже приведены некоторые определения понятия
«резонанс», почерпнутые из Internet:
«Яndex.
1.Словарь по естественным наукам.
«РЕЗОНАНС - резкое возрастание амплитуды вынужденных колебаний
при приближении частоты вынуждающего воздействия к некоторой фиксированной
частоте (резонансной частоте). При наличии трения резонансная частота меньше
частоты собственных колебаний системы»
«Колебания»
Материалы представлены проектом Глоссарий –ru
http://slovari.yandex.ru/art.xml?art=gl_natural/2574/257_4912HTM&encpag...
2. Малый энциклопедический словарь Брокгауза и Эфрона.
«РЕЗОНАНС - физ., усиление звука вследствие передачи звуковых
колебаний другим телам, способным издавать звуки той же высоты и потому
становящимся звуковыми источниками.»
Материалы предоставлены компанией Новый Диск . Издание
1890-1907г.г. http://slovari.yandex.ru/art.xml?art=brokminor/34/34074HTM&encpage=brok...
3. Толковый словарь живого великорусского языка
Владимира Даля.
«РЕЗОНАНС м. франц. зык, гул, рай, отзвук, отгул, гул,
отдача, наголосок; звучность голоса, по местности, по размерам комнаты;
звучность, звонкость музыкального орудия, по устройству его. || В рояле,
фортепьяно, гуслях: дек, палуба, стар. палочка, доска, по которой натянуты
струны.
Материалы предоставлены проектом Рубрикон
Даль В.И. издание 1863-66
©2001 Russ Portal Company Ltd.
http://slovari.yandex.ru/art.xml?art=dal/dal/03151/40800.htm&encpage=dal&...
2. Первичный лингвистический
анализ слова «резонанс».
Первые
попытки перевести это слово на другие европейские языки привели к следующему
результату:
Резонанс – английский – resonance, echo, response.
Резонанс – немецкий – Resonanz, Wiederhall, Echo, Nachklang;
иметь резонанс –Resonanz finden.
Резонанс – испанский- resonancia, repercusion;
иметь большой резонанс – tener gran resonancia.
Резонанс – итальянский - risonanza, ripercussione;
иметь большой резонанс – avere una vasta risonanza.
Обратные переводы на русский язык.
Английский – resonant –
русский а) звучащий, раздающийся, звучный;
б) плавный, назальный;
в) резонирующий, с хорошим резонансом.
Англ. echo – русский-I-существ. 1.эхо, отголосок, подражание.
Syn – imitation
2. подражатель, плагиатор (амер.)
II глагол 1.отдаваться эхом, отражаться.
2. вторить, подражать, поддакивать
Syn. –repeat, imitate.
Эта работа
может быть продолжена практически неограниченно. И её результатом должно стать поле слов,
связанных по смыслу и звучанию с изучаемым нами словом «Резонанс» и явлением,
ему соответствующим.
Предоставляем
читателю возможность выполнить её самостоятельно.
3.
Исследование частоты встречи слова резонанс в Internet.
Одним из
элементов методологии синергетического
исследования всё чаще становится оценка
частоты встречи того или иного слова в Internet
Internet ворвалась
в нашу жизнь как захватчик (внешнее
резонансное воздействие). Предоставляя, казалось бы, неограниченные
возможности для получения необходимой человеку информации, Сеть одновременно
поглощает поверившего ей и часто, наоборот, не позволяет получать необходимые
знания, порождая леность мышления. Однако, процесс взаимодействия Человека и
Сети, который, без сомнения, носит резонансный характер, необратим, и главная
задача - оптимизировать его, повысить его коэффициент полезного действия, чтобы
это резонансное взаимодействие гармонизировало, а не разрушило
взаимодействующие системы – привело к формированию Synergonet [5]-[6].
Статистика
использования того или иного слова в Internet даёт
определённую информацию об его привлекательности и связях c другими
словами и объектами, которые они обозначают. Мы обратились к нескольким
наиболее известным поисковым системам и посмотрели количество ссылок, имеющихся
в этих системах на слово «резонанс» на русском и английском языках. Результаты
представлены в следующей таблице, составленной по материалам Internet от
16.03.2007.
Резонанс Resonance
Yandex. Сайтов 2655.
Страниц 1531371. Сайтов 1502. Страниц
186835
Rambler Сайтов
92842. Докум.1686455. Сайтов 15489. Докум. 278696
Апорт Докум. 339655 Докум. 92751
Google Страниц 2
330000 Страниц 41 400000
Yahoo 1 340000 15 200000
MSN
130446 2
166769.
Анализ
приведённых данных позволяет не только сравнить эффективность различных поисковых
систем при изучении того или иного объекта, но и определить частоту встречи
слова, в данном случае, слова «резонанс». Числа, характеризующие частоту
встречи этого слова в Internet, поражают. Просмотреть все
источники, в которых оно встречается, невозможно. Да это и не требуется. Ведь
большинство из них содержит названия фирм и организаций, взявших на вооружение
это звучное слово.
4.
Смысл, вкладываемый в слово «резонанс» различными авторами.
«Когда исчезнут вещи и дела,
И даже след цивилизаций,
Вдруг прорастут из Времени Слова,
Осмыслив жадное пространство.
Всё, что копили миллионы лет,
Слова вдруг явят,
запах свой и
цвет.
И форму, без которой слова- нет».
З. Е. Журавлёва[7]
Слово
«резонанс» в обыденном понимании означает взаимное усиление функционирования
взаимодействующих структур и систем. Именно поэтому оно часто употребляется в
переносном смысле. Выступление по радио или по телевидению может остаться
незамеченным, а может вызвать «сильный резонанс», то есть значительную ответную
реакцию. Согласованные действия многих людей тоже могут быть названы
резонансными. Представление о резонансе возникает при определенном типе
взаимодействия, когда эффективность совокупной
деятельности взаимодействующих
объектов или субъектов оказывается выше, чем эффективность действия каждого из
них. В таком понимании резонанс становится синонимом синергии – кооперативного
действия нескольких систем с взаимным усилением эффекта. Поэтому в последние
годы изучение резонансных явлений неразрывно связано с Синергетикой – наукой о
самоорганизации сложных систем [8].
5. Простейшее математическое
уравнение, решение которого даёт представление о классическом резонансе.
При научном изучении
этого явления бытовое слово «резонанс» требовалось дополнить формулой,
являющейся решением математической задачи, которая могла бы рассматриваться как
модель одного или нескольких физических явлений. Так оно и произошло в
действительности. Сначала слово «резонанс» описывало процесс усиления звука в
помещениях. Затем это слово стало символом математической формулы, являющейся
особым частным решением обыкновенного дифференциального уравнения второго
порядка с зависящей от времени правой частью. Но одна и та же математическая
формула может описывать различные реальные процессы. И это её свойство стало
играть всё большую роль. Оказалось, что математическое уравнение, моделирующее
явление резонанса, может описывать и усиление колебаний упругих конструкций, и
колебания атомов и молекул, и колебания тока в контуре радиоприёмника, и качку
корабля, и колебания маятника и многие-многие другие явления. [9-15].
Математические
формулы позволили достаточно строго определить понятие «резонанс», отождествив
его с особым решением обыкновенного дифференциального уравнения второго порядка
с постоянными коэффициентами при наличии внешних колебательных воздействий и
при условии близости собственной частоты колебаний с частотой внешнего воздействия.
Это
специфическое математическое уравнение имело столь широкую сферу практического
применения, что слово «резонанс» в своём уже математически строгом определении
стало общепринятым в различных физических, химических и биологических
приложениях. При этом под резонансом понималось усиление колебаний системы под
влиянием внешних воздействий при совпадении частот воздействия и собственных
частот системы.
6. Внутренние резонансы в
системах линейных дифференциальных уравнений с конечным числом степеней свободы
Увеличение
числа переменных в математическом описании линейных колебательных систем
привело к необходимости изучения нового явления, возникающего при сближении
внутренних собственных чисел системы или в случае, если совокупность
собственных частот удовлетворяет определённому резонансному соотношению.
Математические выражения, описывающие это явление, оказались во многом
аналогичными формулам, описывающим явление классического резонанса. Так,
напимер, в многомерных линейных системах было теоретически обнаружено явление вырождения
собственных чисел, которое может считаться одним из проявлений внутреннего
резонанса.
Кроме того,
при анализе нелинейных разложений решений систем обыкновенных дифференциальных
уравнений близи стационарных точек появляется ещё одно понятие внутреннего
резонанса, который возникает при определённом соотношении между собственными
числами матрицы линейного члена разложения [9].
7.
Параметрический резонанс
Математические формулы живут своей, независимой от
приложений жизнью. Они усложняются и модифицируются, и эти модификации отражают
всё более глубокие уровни взаимодействия объектов природы.
Линейное дифференциальное уравнение второго порядка,
на примере которого впервые исследовался колебательный резонанс, является частным
случаем динамической системы, описываемой системой нелинейных дифференциальных
уравнений. В настоящее время колебательные явления, соответствующие этим
уравнениям, согласно [10] могут быть классифицированы следующим образом .
1) собственные колебания ,
2) вынужденные колебания,
3) автоколебания.
При этом, однако, нужно помнить, что
решениями соответствующих уравнений могут быть не только колебательные, но и
экспоненциально растущие и затухающие
движения. Их, следуя [8], будем называть модами.
Собственными или свободными колебаниями или
модами называют такие, которые происходят в системах, не содержащих источников
энергии или эти источники не влияют на протекание процесса.
«Каждую динамическую систему можно
характеризовать набором собственных форм колебаний (мод), называемых
нормальными колебаниями (модами) Число нормальных колебаний зависит от числа
степеней свободы системы. »[10]
Вынужденные процессы реализуются при
наличии непосредственно зависящего от времени внешнего воздействия на динамическую
систему
Именно при изучении вынужденных
процессов (в частности колебаний) и появилась классическая модель резонанса. В
классическом случае зависящее от времени воздействие входит в уравнение в виде
отдельного аддитивного члена, чаще всего описывающего колебательный процесс.
Резонанс возникает тогда, когда собственные (нормальные) моды системы близки
или кратны частоте возмущающего воздействия.
В случае,
если внешнее, зависящее от времени, воздействие изменяет параметры системы, то
обусловленные им возмущения системы называют параметрическими. Усложнение
математических моделей колебательных явлений в сторону учёта дополнительной
зависимости коэффициентов уравнений от времени приводило и приводит к
модификации представлений о резонансе. Явление, названное параметрическим
резонансом, было определено теоретически как особое свойство решения системы
дифференциальных уравнений с зависящими от времени коэффициентами. Подробное
математическое изложение теории параметрического резонанса можно найти в ряде монографий,
среди которых следует отметить [10-15].
Параметрический
резонанс появляется как математическая модель реальных процессов, описываемых
линейными дифференциальными уравнениями с периодическими коэффициентами,
близкими к постоянным. При малом параметрическом возбуждении ранее устойчивая
система может стать неустойчивой (и наоборот). Это имеет место обычно лишь для
некоторых «критических» частот возбуждения, зависящих от нормальных мод
невозмущённой системы уравнений. Теория параметрического резонанса позволяет
определить спектры критических частот и разработать методы построения границ
областей неустойчивости. К необходимости исследования явления параметрического
резонанса приводят многие задачи современной техники и физики (динамическая
устойчивость конструкций в строительной механике, задачи электротехники и
радиотехники, ряд задач космической техники и небесной механики и др.)
В работе [15] В. Н. Челомей привёл несколько
парадоксальных экспериментальных фактов, связанных с параметрическим резонансом.
Вот что он пишет: «Известно, что в
статике центр тяжести механической системы стремится занять устойчивое
положение, при котором потенциальная энергия её приобретает минимальное
значение. Однако в динамике этот общеизвестный принцип иногда нарушается: центр
тяжести системы может занимать динамически устойчивое положение, при котором
потенциальная энергия приобретает значение, близкое к максимальному. Примерами
тому могут служить устойчивое положение «перевёрнутого» маятника с пульсирующей
точкой подвеса или система маятников или
вращающийся гироскоп и др.». Во
всех этих случаях в системах возникает параметрический резонанс.
В
технических приложениях часто используются «параметрические усилители» [10. C.76], то
есть осцилляторы с одновременным использованием параметрического и
классического резонанса.
8.
Нелинейные резонансы в динамических системах. Влияние нелинейности на тип
резонансной кривой. Основные соотношения между возмущающей частотой и
резонансными частотами.
Особой,
бурно развивающейся областью динамики систем с конечным числом степеней свободы
является теория нелинейных колебаний. Существование нелинейных членов в
соответствующих уравнениях приводит даже в случае малых нелинейностей к новым
эффектам. Резонансные явления сохраняются, но они приобретают существенные
особенности, связанные с изменением типов резонансных кривых. Возникают
субгармонические и супергармонические резонансы. Резонансное взаимодействие
проявляется на частотах, в целое число раз больших или меньших частоты возмущающего
воздействия. Эти типы резонансов часто возникают совместно с параметрическим
резонансом, если в нелинейных дифференциальных уравнениях некоторые
коэффициенты периодически зависят от времени.
В системах
связанных нелинейных осцилляторов возникают комбинационные резонансы, то есть
возбуждённые колебания с основными частотами, связанными с частотой возмущения
линейными соотношениями с целыми коэффициентами. Нелинейность способствует
перекачке энергии колебаний из одних частот спектра в другие, что является
очень важным для самоорганизации сложных транспортно-информационных систем.
9. Нелинейные резонансы и
автоколебания.
Одним из
интенсивно развивающихся направлений нелинейной динамики является изучение
нелинейных автоколебательных процессов, связанных с исследованием динамики
активных сред.
Впервые понятие автоколебаний дано А. А.
Андроновым [16-17].
«Автоколебаниями Андронов назвал такие незатухающие колебания в автономной
системе, которые устанавливаются и поддерживаются за счёт внутренних сил,
зависящих от состояния движения самой системы, и амплитуда которых определяется
свойствами системы, а не начальными условиями».[10]
В работах [10, 18-20] приводится
несколько иное определение автоколебаний. «Автоколебательным следует называть
диссипативные динамические системы, в которых могут возбуждаться и существовать
колебания, удовлетворяющие двум требованиям:
1. независимости амплитуды
установившихся колебаний от начального состояния системы в широком диапазоне,
то есть существование в фазовом пространстве системы хотя бы одного аттрактора;
2. независимости или слабой зависимости
спектра возбуждаемых колебаний от спектра источника».
При этом авторы предлагают не
ограничиваться только автономными системами, но рассматривать и системы с
периодическими источниками энергии.
Возникновение
и развитие автоколебаний происходит в условиях, когда потерявшая устойчивость
динамическая система обладает определённым соотношением между собственными
числами. (Этот процесс может считаться также специфическим проявлением
внутреннего резонанса, так как мнимые части одинаково изменяющих свою
действительную часть собственных чисел
имеют разные знаки, но одинаковую величину). Вместо экспоненциального или
степенного удаления от стационарного состояния система переходит к новому –
колебательному состоянию, которое в фазовом пространстве системы описывается в
виде цикла.
Цикл
является простейшим аттрактором, отличным от стационарной точки - стабильного
состояния. Аттрактором называется множество точек в фазовом пространстве, к
которому стремятся со временем все соседние фазовые траектории из некоторой
области, называемой областью притяжения.
Дальнейшее
развитие иерархии неустойчивостей, если они возникают, происходит, хотя и по
различным, но вполне определённым бифуркационным сценариям, проходя бифуркации
удвоения циклов (cценарий Фейгенбаума), рождения
торов различной размерности и, наконец, перехода к хаотическим или
стохастическим странным аттракторам [10, 21-28].
На всех
этапах функционирования автоколебательных систем возможны появления вынужденных
и параметрических резонансов, которые приобретают новые, специфические
свойства. Резонансы могут вызывать бифуркации динамических систем и приводить к
хаотизации динамики системы. Так, например, в работе [29] показано, что в
нелинейном параметрическом усилителе возможна хаотизация колебаний. И
наоборот, стохастические воздействия на систему могут вызвать регулярные
резонансные колебания.
Во многих случаях автоколебательные системы синхронизируются
с частотой вынуждающего воздействия или друг с другом [10].
Таким
образом, изучение нелинейных динамических систем привело к широкому обобщению
математического понятия «резонанс», открытию его новых форм и неограниченному
росту числа приложений, связанных с явлениями, которые с полным основанием
можно было относить к резонансным, хотя ранее они резонансными не
считались. Одновременно расширилось и
количество обиходных явлений, в которых стало использоваться слово «резонанс».
10.Резонансы в системах, описываемых комплексными
уравнениями.
Следует указать на один математический аспект изучения
резонансов в динамических системах. Если дифференциальные уравнения динамики
исследуемого объекта рассматривать в терминах действительных переменных, то
колебательные явления наблюдаются лишь как минимум в уравнениях второго порядка (или двух
уравнений первого порядка). При этом корни характеристического уравнения,
соответствующие колебаниям, являются комплексными. Тем самым, даже оставаясь в
рамках действительных функций, мы вынужденно получаем комплексные
выражения. Однако тот же результат может
быть получен в рамках уравнения первого порядка только не для функции
действительного, а для функций комплексного переменного. Поэтому общий анализ
резонансов целесообразно проводить в рамках комплексных дифференциальных
уравнений [13] при комплексных внешних воздействиях. При таком анализе
выясняется, что вековые члены, соответствующие резонансам, появляются не только
при мнимых, но и при произвольных комплексных
собственных значениях дифференциального оператора. Эти моды формально
также могут считаться резонансными, однако реальное их проявление наблюдать
достаточно сложно на фоне экспоненциального затухания или экспоненциального
роста функций, описывающих решение. И всё же поиск такого рода «резонансов»
представляет интерес. Ведь размножение и рост популяции живых объектов, а также
фазовые переходы из одного стабильного состояния в другое описываются
экспоненциально растущими функциями. Резонансные же возбуждения могут
существенно изменить скорости развития этих процессов и тем самым явиться
орудием управления динамикой системы в период её перехода из одного состояния в другое.
11.
Резонансные явления при произвольных внешних воздействиях.
Резонансные
явления проявляются и при произвольных внешних воздействиях на динамическую
систему. В этом случае внешнее воздействие может быть представлено в виде
интеграла или ряда Фурье, и в случае линейной системы каждая компонента Фурье
воздействует на систему независимо. При этом резонансная компонента вызывает
максимальный отклик. Наиболее отчётливо проявляется этот тип резонанса том
случае, когда наибольшим коэффициентом в разложении Фурье внешнего воздействия
обладает резонансная компонента. Таким образом, реакция, системы, описываемой
математически обыкновенными дифференциальными уравнениями, на произвольное
внешнее воздействие всегда устроена таким образом, что резонансные компоненты
усиливаются и в отклике системы играют большую роль, чем в воздействующем на систему
сигнале.
Математическое
описание резонансных явлений обычно связывают только с дифференциальными
уравнениями. Однако, очень часто динамические системы описываются дискретно, в
виде некоторого итерационного процесса, который лишь в пределе переходит в
непрерывный. Простейшим способом обнаружения резонансных явлений в итерационных
системах может быть дискретизация дифференциальных уравнений, описывающих
резонанс, и их решений. Возможно, на этом пути могут быть сделаны открытия,
подобные открытию фрактальных структур в голоморфной геометрии [30].
12. О
возможности степенных резонансов.
Можно быть
предложено ещё одно важное направление в исследовании временных резонансов. В
качестве примера рассмотрим простейшее комплексное дифференциальное уравнение
первого порядка с экспоненциальным внешним воздействием. Предположим, что в
этом уравнении произведена замена внутреннего
линейного времени на экспоненциальное время [31,32]. Тогда резонансное
решение, записанное в форме колебаний, может быть переписано в виде степенных
функций от экспоненциального (внешнего) времени. Тем самым формально возникает принципиально новый тип
резонансов – степенные резонансы. Особенностью резонансных решений в этом
случае является появление квазистепенных многочленов содержащих логарифмы от
экспоненциального времени.
Специфическая
форма резонансных явлений, приводящая к хаотизации, возникает также при
исследовании возмущений гамильтоновых систем (теория Колмогорова, Арнольда,
Мозера) [10].
Указанные
формы резонансов являются временными резонансами, характеризуемыми
взаимодействием частот и амплитуд линейных и нелинейных колебаний .
Глава II. Волны и волновые
резонансы.
1.
Анализ одномерного линейного волнового уравнения
Специфические
резонансные явления наблюдаются также при взаимодействии волновых движений, так
как любая синусоидальная волна может рассматриваться как бесконечная цепочка
гармонических осцилляторов, каждый из которых может вступать в резонансное
взаимодействие с другими осцилляторами и с внешними возмущениями. Особое,
интенсивно развивающееся направление исследований представляет анализ
взаимодействия цепочек, состоящих из большого числа связанных между собой
осцилляторов, подверженных внешнему воздействию. Здесь проявляются
специфические особенности, которые затем более чётко становятся видны при
анализе волновых движений, а кроме того, возникают резонансные явления, которые
отсутствуют как у систем с малым числом степеней свободы, так и у волновых
систем [10]. Эти особенности могут оказаться важными для
транспортно-информационных систем, имеющих масштабную иерархию осцилляторов или
обобщённых волн. Их использование позволит решить вопрос о масштабных временных
и пространственных резонансах в таких системах и о распределении информации,
массы и энергии на различных уровнях иерархии.
На примере
линейного волнового уравнения с одной пространственной переменной, которое
является математической моделью большого числа природных и социальных явлений,
покажем возможность существования тех типов волновых резонансов, которые
являются аналогами временных резонансов в конечномерных системах.
В случае, если динамика системы
описывается большим числом переменных, благодаря введению дополнительных
гипотез, например, гипотезы эргодичности, удается упростить рассмотрение
поведения динамических систем путем введения небольшого количества новых
осредненных переменных типа плотности, осредненной скорости, тензора
напряжений, температуры, энтропии и новых уравнений связи между этими величинами,
базирующихся на основных законах механики, термодинамики и дополнительных
предположениях о связях между кинематикой движения и тензором напряжений.
Задача исследования динамической системы сводится к исследованию гипотетической
сплошной среды с бесконечным числом скрытых переменных и с конечным числом
функций от пространственных и временной координат, удовлетворяющих системе
уравнений в частных производных. Одним из фундаментальных решений системы
линейных дифференциальных уравнений в частных производных в случае одной
пространственной переменной является решение в виде линейной синусоидальной
волны, описываемой в одномерном случае уравнением:
. (2.1)
Здесь u-скаляр,
характеризующий состояние среды, удовлетворяющий линейному дифференциальному
уравнению в частных производных
, (2.2)
где 
-
линейный дифференциальный оператор с постоянными коэффициентами. Анализ
дифференциального уравнения (2.2) позволяет определить основные параметры волны,
являющиеся общими для всех линейных волн, независимо от их физической природы
(рис. 2.1).
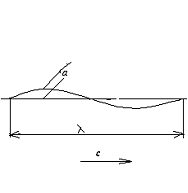
Рис. 2.1. Геометрические параметры волны.
Такими параметрами являются:
амплитуда волны 
;
волновое число 
;
длина волны 
;
угловая частота волны 
;
период волны 
;
cкорость распространения волны 
;
Сумма двух решений
(2.2)
(2.3)
характеризует так называемую стоячую волну, имеющую
точки, в которых 
достигает максимального значения, которые
называются пучностями 
. Решение (2.2) может быть представлено в
комплексном виде:
(2.4)
Подстановка уравнения (2.4) в (2.2) приводит к
дисперсионному соотношению:
. (2.5)
Уравнение
(2.5) может иметь конечное или бесконечное число решений, определяющих
зависимость между частотой волны и волновым числом.
Каждое решение может быть записано в виде:
(2.6)
Если задаться величиной , то
определяется из (2.6) и формула (2.4) может
быть записана в виде:
. (2.7)
При рассмотрении двух гармонических бегущих волн
(2.8)
в результате их
суммирования получаем так называемые биения
. (2.9)
Если построить график функции , то
получим картину, изображённую на рис. 2.
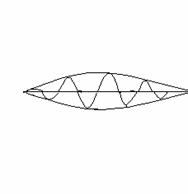
Рис. 2
Биения.
Волны с частотой 
и волновым числом 
распространяются группами. При этом скорость
распространения амплитуды группы отличается от скорости распространения каждой
отдельной волны. Наряду с фазовой скоростью распространения волны
при 
(2.10)
возникает
групповая скорость 
. Если 
, то
фазовая и групповая скорости волны совпадают. В противном случае скорость волны
зависит от ее частоты - такие волны называются диспергирующими. Общее решение волнового
уравнения (2.2) получено и исследовано в ряде работ и монографий, в частности,
в монографии [33]. Подробный анализ линейных трехмерных диспергирующих волн дан
в монографии [34]. Там же изложена теория источников пространственных волн в
сплошной среде. Аналогичные исследования линейных волн в сплошных средах в
электродинамике и оптике изложены в ряде учебников, (см. например [35], [36].
Линейные волны представляют собой широкий глубоко изученный класс волновых
движений.
Можно ввести для незатухающей линейной
волны аналог фазовой плоскости, а для системы волн аналог 2n-мерного фазового
пространства. Введем такое пространство сначала на примере простейшей линейной
синусоидальной волны, описываемой уравнением (2.1). Здесь возможны два подхода.
Первый подход соответсвует введению новой системы координат - волновой
, (2.11)
в которой волна остаётся стационарной или меняется
слабо. В этом случае
.
(2.12)
Если мы рассмотрим, как и ранее, незатухающую волну,
то в волновой системе координат она представляет собой стационарную структуру
. (2.13)
Однако пространственная бесконечномерность волны
проявляется в том, что стационарная структура имеет протяженность в
пространстве, задаваемую уравнением (2.12).
Другим возможным способом является введение для каждой
волны трехмерного фазового пространства. Кроме функции 
вводятся в рассмотрение две ее частные
производные - 
и 
. Одномерное линейное уравнение в частных
производных с постоянными коэффициентами
, (2.14)
решением которого является синусоидальная волна,
распространяющаяся со скоростью 
, записывается в виде системы из трёх уравнений
(2.15)
(2.16)
, (2.17)
где
(2.18)
Если теперь
построить фазовую траекторию системы (2.15) - (2.18) в трехмерном фазовом
пространстве для синусоидальной волны, то получим эллипс, лежащий в плоскости,
проходящей через ось и пересекающий плоскость 
под углом, тангенс наклона которого к оси 
равен 
.
Такой подход позволяет описать бесконечномерную систему одной линией в
трехмерном пространстве и провести дополнительную аналогию между колебаниями и
волнами (смотри рис.3).
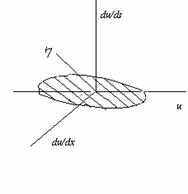
Рис.2.3.
Фазовое трехмерное пространство одномерной волны.
Одна из полуосей эллипса равна максимальному значению , а
другая полуось определяется как корень квадратный из суммы квадратов
максимальных значений 
Выполним
замену переменных:
(2.19)
,
где
(2.20)
В плоскости
фазовой тректории волны 
.
Введем новую фазовую координату 
,
определяемую соотношением
. (2.21)
Таким образом, введение новых переменых 
позволяет перейти к новой плоскости 
, в
которой фазовое описание синусоидальной волны становится эквивалентным фазовому
описанию колебательного движения(смотри рис.2.4).
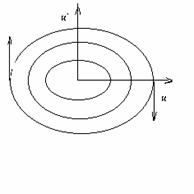
Рис. 2.4.
Фазовая плоскость одномерной волны в плоскости 
.
Это описание легко может быть обобщено
на случай установившихся волновых движений с постоянной скоростью и на любое конечное
число волн. Построенная картина полностью аналогична фазовой картине свободных
колебаний. Эта аналогия позволяет в некоторых случаях обобщать на волновые
движения качественную теорию обыкновенных дифференциальных уравнений
Таким образом, линейное дифференциальное
уравнение в частных производных с постоянными коэффициентами, нулевой правой
частью и безграничной областью определения может быть решено в общем виде. Для
него может быть получена определённая совокупность дисперсионных соотношений,
характеризующих параметры линейных волн, которые являются решениями этих
уравнений. Задаваясь начальными условиями, можно получить решение в виде
интеграла Фурье от волновых гармоник, частота и волновое число каждой из
которых удовлетворяют исследуемому волновому уравнению. При этом существенную
роль начинает играть волновая дисперсия, то есть зависимость частоты волны от
волнового числа [33].
Выше были рассмотрены только свободные
волны. Однако, так же, как и в случае одномерных и многомерных колебаний, могут
существовать и вынужденные волны. Следуя сценарию, отработанному в теории
конечномерных систем, можно ввести на уровне анализа линейных и нелинейных
волновых уравнений все типы резонансов, которые наблюдались у систем с конечным
числом измерений.
Дисперсионные
соотношения, полученные в результате анализа дифференциального уравнения в
частных производных для различных корней дисперсионного уравнения (2.5) могут
оказаться близкими, так что одному волновому числу будут соответствовать
близкие частоты, что может привести к появлению в функции, описывающей решение,
вековых членов как по временной, так и по пространственной координатам.
Возникают биения, а в предельном резонансном случае амплитуда волн линейно по
временной и пространственной координатам стремится к бесконечности. Это явление
также может считаться резонансным и по аналогии с резонансом в конечномерных
динамических системах названо нами внутренним волновым резонансом..
Другим типом
волнового резонанса может служить вынужденный резонанс, когда в правой части
волнового уравнения стоит выражение,
представляющее произведение константы на комплексную экспоненту от суммы
частоты, умноженной на время и волнового числа - на координату.
В этом случае волновое движение может быть так же, как
и в случае конечномерных систем, представлено в виде суммы собственных и
вынужденных волн, при этом, если частотные и (или) геометрические параметры
возмущающей волны окажутся совпадающими с параметрами одной из спектра
возможных собственных волн системы, то амплитуда именно этой волны начнёт
интенсивно расти, и возникает вынужденный волновой резонанс. Так как
произвольное внешнее возмущение, распределённое в пространстве и зависящее от времени может быть
представлено в виде интеграла Фурье, то вынужденный волновой резонанс можно искать при произвольном
внешнем волновом воздействии.
Так же
изучается волновой параметрический резонанс, когда коэффициенты волнового
уравнения периодически зависят от временной и пространственной координат.
Переход к
волновым явлениям порождает идею о возможности не только колебательных
временных, но и пространственных резонансов. В простейших линейных волновых
уравнениях пространственная и временная координаты входят в уравнение
симметрично. Следовательно, если правомочно провести сечение волнового решения
по пространству и в некоторой точке рассматривать колебательное движение во
времени со своими резонансными значениями искомых параметров, то с таким же
успехом возможно выполнить сечение по времени и рассматривать мгновенную
картину волнового движения в пространстве - построить в этом пространстве
колебательную картину и, написав соответствующее дифференциальное уравнение,
также искать резонансные волновые числа. Это утверждение играет конструктивную
роль при анализе квазистационарных решений волновых уравнений в системе
координат, связанной с движущейся волной.
Так же, как
и при исследовании конечномерных динамических систем, существенное влияние на
поведение сплошных сред, описываемых волновыми уравнениями, оказывает
нелинейность, которая кроме проявлений, аналогичных проявлениям, известным
для конечномерных динамических систем,
имеет свой, специфический характер.
Поэтому,
прежде, чем рассматривать нелинейные волновые резонансы, рассмотрим типы
нелинейности присущие волновым структурам, принципиально отличающие их от
стандартных конечно-мерных динамических систем.
2. Классификация нелинейных
волн, структур и систем.
Существует
большое число учебников и монографий, посвящённых результатам теоретических и
экспериментальных исследований волновых движений различной природы. Однако, в
большинстве из них отсутствует понятие «волна». Чаще всего это понятие
отождествляют с уже рассмотренными нами ранее линейными волнами. Однако,
исследования последних десятилетий показали, что учёт нелинейности позволяет
практически неограниченно расширить представление о волне. Наиболее общее из
известных нам определений дано в монографии [33] « … в самом общем случае мы
определим волну как пространственно - временную эволюцию некоторого состояния».
Это определение характеризует основное свойство волны, которое остаётся
неизменным независимо от типов волн, которые рассматриваются. А именно то, что
при описании волновых движений мы следим не за частицами среды, в которой
распространяется волна, а за параметрами или совокупностью параметров, которые
описывают состояние среды. Эти параметры остаются постоянными или меняются по
заданному закону в точках, которые считаются принадлежащими к волне.
Это общее
определение явилось следствием интенсивного развития за последнее время
исследований нелинейных процессов в различных областях знаний и обнаружения
волновых свойств у таких нелинейных процессов и структур, которые ранее не
считались волновыми. В статье Ю. А. Данилова и Б. Б. Кадомцева «Что такое
Синергетика», открывающей сборник [36. С. 9], говорится: «Отечественная школа
нелинейных колебаний и волн, основоположником которой по праву считается Л. И.
Мандельштам, рассматривает общую теорию структур в неравновесных средах как
естественное развитие и обобщение на распределённые системы идей и подхода
классической теории нелинейных колебаний. Ещё в тридцатых годах (прошлого века) Л.И. Мандельштам
сформулировал программу создания нелинейной культуры, включающей надёжный
математический аппарат и физические представления, адекватные новым задачам,
нелинейную интуицию, выработанную на нелинейных задачах».
Близкое
мнение высказано в обширной монографии по нелинейной теории колебаний и волн,
написанной одной из выдающихся представителей
Российской школы нелинейных колебаний П. С. Ланда [10. С.11]: «Теория
колебаний и волн – это наука, изучающая колебательные и волновые движения
независимо от их физической природы. Под колебательными движениями мы, согласно
Л. И. Мандельштаму, будем понимать всякие происходящие длительное время
ограниченные изменения состояния тела. В силу ограниченности эти изменения
обязательно должны происходить туда и обратно [10]. Под волновыми движениями мы
будем понимать колебательные движения, распространяющиеся в пространстве. Из
этих определений видно, что изучение колебательных и волновых движений должно
быть взаимосвязано, то есть разделение теории
колебаний и теории волн, как это часто делается, не является
оправданным. Данное определение теории колебаний и волн является очень широким»
Ю. А.
Данилов и Б. Б. Кадомцев [37] указывают, что Л. И. Мандельштам предупреждал о
ненужности на определённом этапе исследований строгих определений всех понятий
в нелинейной науке. Мы полностью присоединяемся к его мнению и считаем, что в
настоящее время ещё нет необходимости в абсолютно точном определении понятия
«волна» (так же, как и понятий структура, система, процесс, явление, событие).
В последние
годы исследования нелинейных процессов привели к развитию новой науки - синергетики – науки о самоорганизации
материи. Как показали многочисленные
исследования, при изучении вопросов, связанных с формированием новых структур и
систем, на первый план выступают их характерные волновые черты: слабая
зависимость их пространственных и временных параметров от начальных условий и
геометрических размеров системы.
Такой подход
позволил значительно расширить представление о волновых процессах и ввести
классификацию волновых движений, структур и систем, опирающуюся на их общие
волновые свойства, в рамках которой удалось проследить за характером влияния
нелинейности на переход классических линейных волновых движений в динамические
структуры и сложные самоорганизующиеся транспортно-информационные системы [31],
[38 - 46].
Классификация проводится по трём параметрам.
1. Классификация по типу:
а. Обобщённые волны, представляющие собой классы
идентичных объектов (квантов).
б. Вероятностные волны, характеризующие изменение
плотности вероятности отыскания системы или структуры в одном из возможных для
неё состояний из континуума возможных состояний системы.
в. Классические волны в сплошной среде,
характеризующие изменение во времени и пространстве плотности какого-либо
параметра или связанной между собой совокупности параметров сплошной среды.
2. Классификация по характеру взаимодействия с другими
системами, аналогичная рассмотренной нами ранее классификации конечномерных
динамических систем:
а. Свободные (собственные) волны.
б. Вынужденные волны.
в. Автоволны.
3. Классификация по степени нелинейности [31, 39, 41,
45, 46].
а. В качестве первого класса рассматриваются все волны
относительно малой амплитуды, математическое описание которых в одномерном
случае кратко представлено выше в виде совокупности решений линейных волновых
уравнений в частных производных.
б. Ко второму классу, названному нами умеренно -
нелинейными волнами, отнесены различные формы ударных волн в сплошных средах,
солитоны, а также скачки тех или иных параметров в однородной среде и границы
раздела сред. В качестве подкласса данного класса могут быть рассмотрены
автоволны в активных средах [47], диссипативные континуальные структуры и
структуры, формируемые в результате возникновения режимов с обострением [48].
Умеренно-нелинейные волны часто являются границами некоторых объёмов, которые
они отделяют от окружающей среды – поля. Такие объёмы мы будем называть
телами-волнами.
в. К третьему классу, названному нами вихревыми
ударными волнами, отнесены вихревые и
(или) спиральные структуры, формируемые вследствие пространственной потери
устойчивости фронта и формы умеренно нелинейных волн. В частности, сюда
относятся специфические автоволновые образования, называемые ревербераторами
[47].
г. К четвёртому классу, названному грибовидными
структурами, отнесены структуры мультипольной природы, формирующиеся из
вихревых и спиральных структур. Различные модификации и комбинации структур
такого типа составляют основу практически всех объектов живой и неживой
природы.
д. К пятому классу отнесены структуры, названные нами
древовидными, геометрия и бифуркационная динамика которых может быть описана
методами математической теории графов, в частности, теории математических
деревьев [49].
е. К шестому классу мы отнесли сложные, в том числе
самоорганизующиеся системы, названные транспортно - информационными, и
являющиеся, в основном, результатом трансформации и взаимодействия грибовидных
и древовидных структур, а также волновых движений и структур более низких
классов.
Несмотря на
то, что четвёртый, пятый и шестой классы структур и систем встречаются и в
неживой природе, наиболее широко они распространены в технических,
биологических и социальных системах. Поэтому общие закономерности их динамики
оказываются важными не только для физики и химии, но и, главным образом, для
технических приложений, наук о Земле, биологии и наук о человеке и обществе.
Рассмотрим объекты предложенной классификации
несколько более подробно.
3. Умеренно - нелинейные волны.
Некоторым линейным волновым уравнениям можно
сопоставить соответствующие нелинейные уравнения. В качестве примера вновь,
следуя [33], рассмотрим одномерные уравнения первого порядка.
Простейшие линейные уравнения. I класс:
a) 
b) 
(2.22)
c) 
Соответствующие им нелинейные уравнения. II класс:
a) 
-
уравнение Пуассона-Римана;
b)
-
уравнение Бюргерса; (2.23)
с) 
- уравнение Кортевега-Де-Фриза.
Если уравнение (2.22 a) описывает
произвольную стационарную волну, то уравнение (2.23 а) [33] , например, при
начальных условиях:
(2.24)
имеет решение :
, (2.25)
где 
пространственная координата, движущаяся со
скоростью (которая в свою очередь сама является функцией
от 
и 
). Eсли
функция 
имеет производную 
при 
в точке , то
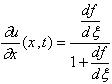. (2.26)
Если 
, то
бесконечна при 
. Нелинейность приводит к деформации волнового
профиля, возрастающей с ростом .
Если 
, то решение уравнения (2.23а) становится
многозначным. Физически это приводит к появлению в сплошной среде движущихся
разрывов. Такие типы движений в механике сплошной среды называются простыми
волнами. Подробное исследование разрывов в трёхмерной сплошной среде было
выполнено в работах Ж.Адамара, Н.Е.Кочина, К.Трусделла [50-52] и других
авторов, в которых рассмотрена классификация и изложены общие свойства
сингулярных поверхностей - поверхностей разрыва.
В общем виде уравнение движения сплошной среды имеет
вид:
(2.27 )
где 
- радиус-вектор материальной точки в
абсолютной системе координат; 
-вектор
лагранжевых координат точек сплошной среды. Тогда поверхность в отсчётной
конфигурации или её образ в текущей конфигурации движущегося тела называется
сингулярной поверхностью (или волной) 
-го
порядка, если она сингулярна по отношению к некоторой -ой
производной скалярного, векторного или тензорного поля 
(то есть на этой поверхности функция или её
производная, описывающие поле, терпят скачок), определяемого в пространстве,
занятом сплошной средой. Cингулярные поверхности порядков 0 и 1 называются
сильными: к ним относятся математические
абстракции типа классических ударных волн нулевой толщины, бесконечно тонких
вихревых пелен, о формировании которых мы будем говорить позднее, разрывы и
поверхности контакта двух тел, фазовые границы. Сингулярные поверхности порядка
2 и выше называются слабыми. Фактически к сингулярным поверхностям относятся
любые скачки параметров в сплошной среде, любые процессы, связанные с фазовыми
переходами в сплошных средах. При этом локально в направлении, нормальном к
сингулярной поверхности, параметр, терпящий скачок, удовлетворяет нелинейному
уравнению типа:
, (2.28)
где 
- проекция градиента величины на нормаль к сингулярной поверхности. В обшем
случае
может быть произвольной функцией, в том числе,
равной нулю или константе. Уравнение (2.28)
может быть заменено локально любым из уравнений (2.23b)-(2.23c) или их
обобщений [33, 47, 48]. Тем самым, объединяя путём сращивания различные типы
внутренних одномерных нелинейных волн с внешним анализом сингулярных
поверхностей в сплошной среде и предлагая конструктивный способ изучения зон
резких изменений в сплошной среде, мы тем самым можем ввести в рассмотрение
наряду с классом линейных волновых движений, новый широкий класс нелинейных
волновых структур, которые могут быть названы нелинейными обобщенными ударными
волнами или умеренно-нелинейными волнами.
Поясним возможный алгоритм
асимптотического анализа нелинейных обобщённых ударных волн. Если в сплошной
среде формируется или имеется не скачок, а зона резкого перехода от одного
значения параметра к другому, ширина которой значительно меньше радиуса
кривизны этой зоны, то перемещение свойств среды вблизи этой зоны можно назвать
трехмерной ударной волной. Все соотношения, полученные для сингулярных
поверхностей, в первом приближении оказываются справедливыми и для этого
случая. При этом для анализа поля вблизи зоны резкого скачка параметров в ряде
случаев локально оказывается справедливым нелинейное уравнение, являющееся
обобщением уравнения Бюргерса, которое может быть переписано в форме
(2.29)
Особенность уравнения (2.29) заключается
в том, что оно может иметь несингулярное стационарное решение, которое,
например, в случае 
имеет вид.
(2.30)
(2.31)
Здесь 
определяются из решения внешней задачи в
приближении сингулярных поверхностей
(2.32)
На языке
аэродинамики полученное решение описывает структуру ударной волны. Главный
вывод, сделанный для одномерного движения и являющийся, как следует из
предыдущего анализа, общим, состоит в следующем [33]: "Нелинейность
уравнения Бюргерса позволяет гладко соединить два асимптотически однородных
состояния (разрыв) c помощью непрерывно изменяющихся состояний. Член второго
порядка стремится нейтрализовать влияние нелинейности в области, где возможно
появление сингулярности, и сгладить разрывы."
Если 
, мы
вновь возвращаемся к сингулярным поверхностям.
Замена переменных позволяет линеаризовать уравнение
Бюргерса и свести его к линейному уравнению теплопроводности, что позволяет
изучать взаимодействие нелинейных ударных волн [10].
Сочетание в
волновых уравнениях членов, определяющих дисперсию, с нелинейными членами
порождает наряду с обычными волнами удивительные объекты - уединённые волны или
солитоны, открытие которых имеет почти двухвековую драматическую историю, и не
все свойства которых изучены полностью.
« … в реальных системах спустя некоторое
время устанавливаются и довольно долго существуют волны, по форме близкие к
солитонам. В дальнейшем эти волны медленно затухают. Красочное описание
образования такой волны в воде перед остановившейся внезапно баржой и
последующего её поведения дал Джон Скотт Рассел [53-54], который наблюдал это
явление ещё в 1834 г.: «Я следил за движением баржи, которую быстро тянула по
узкому каналу пара лошадей, когда баржа неожиданно остановилась; вместо этого
она собралась около носа судна в состоянии бешеного движения, затем неожиданно
оставила его позади, катясь вперёд с огромной скоростью и принимая форму
большого одиночного возвышения, т. е. округлого, гладкого и чётко выраженного
водяного холма, который продолжал свой путь вдоль канала, нисколько не меняя
своей формы и не снижая скорости. Я последовал за ним верхом, и когда я нагнал
его, он по-прежнему катился вперед со скоростью приблизительно восемь или
девять миль в час, сохранив свой первоначальный профиль возвышения длиной около
тридцати футов и высотой от фута до фута с половиной. Его высота постепенно
уменьшалась, и после одной или двух миль погони я потерял его в изгибах
канала.»[10]
Солитоны
обладают многими свойствами, которые до их открытия приписывались частицам.
Одновременно их можно считать специфическими размытыми ударными волнами.
Солитоны появляются как устойчивые
решения различных дифференциальных уравнений, описывающих, казалось бы,
не связанные между собой явления природы. В их формировании и их свойствах есть
нечто загадочное, что привлекло к их исследованию крупнейших учёных [10], [33].
Можно
считать, что при формировании солитонов проявляется специфическая форма
нелинейного резонанса между членами дифференциального уравнения, которое их
описывает: дисперсионные члены вызывают расхождение в пространстве
диспергирующих волн с различными волновыми числами, тогда как нелинейность
приводит при определённых условиях к концентрации в одной точке максимумов волн
различной частоты. Эти два эффекта уравновешиваются в солитоне и формируют
устойчивую структуру, переносимую в пространстве с постоянной скоростью практически
без изменения её формы
Динамика солитона, в частности,
описывается уравнением Кортевега-де-Фриза рядом его аналогов [33, 55-65]. Вслед за [33] выпишем одно из
стационарных решений уравнения (4.39с)
, (2.33)
где
(2.34)
(2.35)
а 
-эллиптические
функции Якоби (
-функция,обратная
к 
).
-вещественные
корни уравнения
(2.36)
A и B-постоянные интегрирования, определяемые
условиями на бесконечности.
Функция 
,
описываемая уравнением (2.33), является периодической нелинейной волной с
периодом
, (2.37)
где 
-полный
эллиптический интеграл первого рода:
.
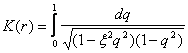Из-за наличия
функции 
в выражении (2.33) нелинейная волна, описываемая этой формулой,
называется кноидальной. Если 
, то
формула (2.33) принимает следующий вид
(2.38)
(2.39)
Период волны,
описываeмой равенствами (2.38) и (2.39), оказывается равным бесконечности.
Устремляя к 
,получаем:
(2.40)
и
окончательно:
(2.41)
Уравнение
(2.41) - уравнение уединённой волны-солитона. Обнаруженные экспериментально
Скоттом Расселлом (1844) [53-54]. и исследованные математически Кордевегом и Де
Фризом [55], солитоны долгое время не привлекали внимания исследователей, пока
в 50-х, 60-х годах аналогичное уравнение не было обнаружено при исследовании
плазмы [56]. Затем поток исследований солитонных решений различных нелинейных
уравнений возрастает вплоть до настоящего времени экспоненциально [57-65].
Подробный список работ, посвящённых исследованию солитонных решений различных
уравнений имеется в [10],[63],[64].
Если рассмотреть солитонное решение
уравнения Кортевега-Де-Фриза как первый член внутреннего разложения какого-либо
трёхмерного разрывного движения, как это мы сделали ранее для ударных волн, то
при асимптотическом анализе внешнего решения можно рассматривать такую
структуру как частный случай сингулярной поверхности минус первого порядка, то
есть как особую форму слияния двух близко расположенных скачков. Качественно
аналогичный результат можно получить, если при анализе ударных волн
рассматривать не саму функцию, а её производную по нормали к фронту волны.
Таким образом, солитонное решение может быть естественным образом включено во
введённый нами класс обобщённых ударных волн как нелинейная ударная волна минус
первого порядка (так же как и режимы с обострением, хотя характер локального поведения основной меры в
районе обострения существенно отличается).
Между поведением
решений уравнений типа Кортевега-де-Фриза и типа Бюргерса имеется
принципиальное различие, определяемое порядком высшей производной и связанное с
диссипацией энергии волн. Однако, это отличие не столь велико, чтобы
воспрепятствовать включить все рассмотренные выше и аналогичные им нелинейные
волны в один класс. Существуют волновые движения, являющиеся переходными от
линейных синусоидальных волн к волновым структурам второго класса (например,
кноидальные волны).
Сингулярные границы, обобщение которых в
виде умеренно нелинейных волн дано выше, обычно представляют собой замкнутые
поверхности, отделяющие внутреннюю часть пространства от остального мира. Эта
замкнутая часть пространства может быть названа телом-волной. Большинство
предметов окружающего мира может быть отнесено именно к этому классу..
Таким
образом, специфическими особенностями, существенно отличающими их от
соответствующих решений систем обыкновенных уравнений, могут обладать решения
некоторых нелинейных уравнений в частных производных, порождающих совершенно
новые явления, связанные с зависимостью искомых параметров движения от
пространственной координаты. Нелинейные члены типа произведения некоторой
функции искомой величины (или совокупности искомых величин) на её производную
по пространственной координате порождают во взаимодействии с линейными и
нелинейными членами уравнений, описывающими дисперсию и диффузию, такие новые
структуры и явления как ударные волны,
солитоны, автоволны, диссипативные структуры, режимы с обострением. Появление
ударных волн физически означает формирование в сплошной среде движущихся
разрывов, что является проявлением одного из важнейших нелинейных механизмов
рождения границ в сплошной среде. Наличие процессов такого типа позволяет рассматривать резкие и размытые скачки параметров в сплошных
средах как обобщённые ударные волны и относить их также ко второму классу –
умеренно - нелинейным волновым системам.
Уравнения
теплопроводности и Бюргерса представляют простейший пример класса
параболических нелинейных дифференциальных уравнений в частных производных,
описывающих широкий круг процессов: и образование турбулентности, и химическую
кинетику в условиях конвекции, и распространение волн в активных средах…
В одномерном случае общий вид этих уравнений запишется
следующим образом:
.
(2.42)
В некоторых случаях нелинейности, определяемые
неоднородностью среды, в которой формируются нелинейные волны, или её
активностью, порождают в среде процессы, приводящие к неограниченному росту
параметров возмущения. Иногда этот рост значительно более интенсивен, чем рост
возмущений при исследовании экспоненциальной неустойчивости динамических
систем. Такие явления С.П. Курдюмов назвал режимами с обострением [48]. Хотя
эти режимы и существенно отличаются от ударных волн и солитонов, однако, по
нашему мнению, их также можно отнести к умеренно- нелинейным волнам.
Скорость
перемещения умеренно - нелинейных волн так же, как и линейных, может меняться в широких пределах.
Так, например, если умеренно-нелинейная волна является границей неподвижного
твёрдого тела, то её скорость равна нулю. В этом случае граница является
замкнутой. Она отделяет внутренность тела от внешней среды – поля.
Совокупность
умеренно-нелинейной волны и объёма, отделённого ею от окружающего пространства,
будем называть телом-волной.
Глава III. Вихревые и
грибовидные структуры.
Транспортно-информационные системы.
1. Вихревые ударные волны
первого рода. Формирование вихревых
пузырей. Ревербераторы.
Условия формирования следующего класса
нелинейных волновых структур определяется, главным образом, особенностями
взаимодействия умеренно - нелинейных волн со средой, их окружающей. Частным
примером такого взаимодействия являются поверхностные волны на границе раздела
сред. Классические линейные волны на поверхности воды являются результатом
взаимодействия границы раздела (умеренно-нелинейной волны) с жидкостью,
подверженной действию сил тяжести. Как известно, на границе раздела сред
возникают волновые деформации, в первом приближении представляющие собой
двумерные диспергирующие линейные волны. Изучению этих волн в настоящее время
посвящена обширная литература, например [34], [65-67]. Увеличение энергии
гравитационных волн на поверхности воды приводит к появлению существенных
нелинейных эффектов, связанных с взаимодействием границы со средой.
Это нелинейное взаимодействие подробно изучено
математически. Выполненные исследования [65 - 67] показывают, что на свободной
поверхности могут реализовываться, в зависимости от относительной глубины
погружения, вычисленной по длине волны, два типа симметричных нелинейных волн:
при малых глубинах водоёма - кноидальные и уединённые волны солитонного типа, а
при значительных глубинах - волны Стокса. Несмотря на отличие этих двух типов
волн, между ними имеется много общего, связанного с нелинейностью:
а)
происходит выполаживание подошвы и заострение вершины волны, при этом профиль
волны в случае больших глубин водоёма с увеличением амплитуды стремится к форме
предельной волны Стокса с угловой критической точкой в вершине [65], что
приводит к качественно новым бифуркационным явлениям;
б) на
свободной поверхности увеличивается модуль абсолютной скорости частиц жидкости
(у предельной волны Стокса в критической точке скорость жидкости становится
равной скорости перемещения волны).
Тем самым,
на границе между жидкостью и газом наряду со скачком плотности возникает и
становится всё более интенсивным скачок завихрённости.
Cвязь между
нормальной и касательной составляющими вектора, параметры которого определяют
свойства сингулярной поверхности, описывается соответствующими интегральными
уравнениями, ядрами которых являются фундаментальные решения уравнений
математической физики для среды, формирующей тело-волну. Нелинейность волн
деформации границ раздела сред наряду с умеренно-нелинейными волнами приводит к
появлению нового типа волновой картины: Стоксовой волны с угловой точкой, -
появляется возможность принципиально новой геометрической трансформации границы
- потеря аналитичности её формы, появление угла - излома фронта волны.
Аналогичные особенности (каустики) [34],
[68] появляются и при пространственном анализе фронтов классических линейных
волн, однако там они обычно не сопровождаются скачками завихрённости и
формированием спиральных структур, составляющими основные особенности
процессов, которые будут изучаться нами ниже. Теория каустик волновых фронтов в
настоящее время интенсивно изучается физиками и математиками. Она оказывается
тесно связанной с теорией особенностей лагранжевых многообразий и теорией
катастроф [68].
Итак, основным следствием нелинейных
взаимодействий, приводящих к формированию следующего класса волновых структур,
является порождение на волновых фронтах интенсивной завихрённости,
распределение которой в пространстве или на плоскости приводит к существенным
нелинейным эффектам и порождает новые
структуры, которые начинают жить по собственным законам, взаимодействуя
с породившей их средой. К этому же классу могут быть отнесены и структуры,
которые представляют зоны концентрации ротора любого вектора, не обязательно
вектора скорости сплошной среды.
Порождение и диффузия завихрённости,
наиболее интенсивно проявляющиеся на контактных поверхностях, отнесённых нами к
умеренно нелинейным волнам, значительно усложняет их структуру, формирует новые
типы обобщённых ударных волн: пограничные слои резких градиентов касательных
составляющих вектора, Существенно нелинейный характер вихревых волн, скорость
перемещения которых может совпадать со скоростью перемещения среды, в которой
они возникают (то есть собственная скорость может стать равной нулю), приводит
к возникновению нового класса нелинейных вихревых структур, которые, сохраняя
свойства породивших их классических линейных и умеренно - нелинейных волн,
оказываются значительно ближе к телу-волне, то есть формируют устойчивые
слабодеформируемые структуры, переносящие не только свою форму, но и большую
часть массы среды, в которой они формируются.
Проанализируем возможные пути
формирования и основные топологические свойства вихревых (или в более общем
случае - роторных) структур. Если в качестве модели рассмотреть линейные
поверхностные волны на границе раздела двух сред и рассчитать в рамках
допущений невязкой жидкости скачок касательных
скоростей, то этот скачок, хотя и существует, но очень мал. С увеличением
нелинейности интенсивность сдвигового слоя растёт. Предельная Стоксова волна
уже в значительной степени вихревая. Вблизи критической точки (вершины) интенсивность завихрённости максимальна.
Дальнейшее развитие влияния нелинейности на характеристики поверхностных волн происходит по другим
законам - законам вихревых ударных волновых структур.
В работе [38] одним из авторов совместно
с Н. Ю. Завадовским рассмотрена простейшая модельная задача, решение которой
вскрывает механизм развития на границе раздела сред новых вихре - волновых
структур и объясняет качественно один из элементов сложного нелинейного явления
- спирализации нелинейных волн на границе раздела сред. Если проанализировать,
при допущении о пренебрежении нормальными к границе скоростями по отношению к
касательным, поведение свободной первоначально гладким образом искривленной
границы раздела сред без учета действия сил тяжести, то математическая
постановка такой задачи для невязкой жидкости постоянной плотности сводится к
уравнению Лапласа внутри жидкости и к уравнению Пуассона-Римана (2.23 а) для
скачка касательных скоростей на деформируемой границе раздела.
Совместное рассмотрение этих связанных между собой
уравнений приводит к аналитическому решению, форма которого показывает, что на
свободной границе через конечный промежуток времени формируется продольная
поверхностная ударная волна - появляется отсутствовавший ранее скачок
продольных касательных скоростей - что приводит к скручиванию самой границы в
двойной спиральный вихрь с бесконечным числом витков [69 - 72] (рис.3.1)
Рис.3.1
Формирование
двойного спирального вихря.
Удалось
построить стационарные двумерные течения идеальной жидкости, которые можно
классифицировать как обобщения двойного спирального вихря. Если ввести при
рассмотрении двумерных потенциальных потоков с границей следующие комплексные
функции:
(2.43)
и рассмотреть стационарное течение, а затем определить
уравнение связи
(2.44)
то получим спектр течений, представляющих потоки
вблизи угловых точек, либо внутри двойных спиральных вихрей. Примеры таких структур представлены на рис. 3.2.
Рис.3.2
Различные типы вихревых ударных волн первого рода
В действительности, однако, так же как и
в случае ударных волн, происходит диффузионное и хаотическое размывание как в
касательном, так и в нормальном направлении указанных идеальных структур, наиболее
интенсивноe внутри центральных областей спиралей.
Совокупность формирующихся, стационарных
и диссипирующих структур этого типа названа нами вихревыми ударными волнами
первого рода. Они обычно являются элементами таких сложных физических явлений,
как разгонные вихри за крылом, отрывные пузыри на телах, концевые вихри на
крыльях, дорожки Кармановских вихрей за плохообтекаемыми телами и паровыми и
газовыми кавернами и т. д.
Если рассматривать подобные структуры с
топологической точки зрения и учесть диффузию завихрённости при их
формировании, то их скорее можно считать телами - волнами, чем
умеренно-нелинейными волнами, хотя формируются они в районе фронтов
умеренно-нелинейных волн. Именно формирование из умеренно-нелинейных волн
вихревых ударных волновых структур первого рода и является тем качественным
скачком, который позволяет выделить третий класс - нелинейные вихре -волновые и
спиральные структуры - вихревые ударные
волны первого рода.
Если размеры введенных ранее в
рассмотрение тел - волн определяются параметрами их границ, то вихревые ударные
волны первого рода фактически являются одновременно и частью границы
какого-либо другого тела - волны, и сами
по себе вновь сформировавшимися из этой границы телами - волнами. Главной их
особенностью как вихревых структур является наличие на какой - либо из стадий
их формирования спиральных волн.
К этому же классу могут быть отнесены
ревербераторы [47. C. 129, которые могут быть названы спиральными авто -
волнами.
2.
Вихревые ударные волны второго рода. Вихревые пелены.
Анализ топологических свойств линий и
поверхностей обусловливает еще один вид формирования вихре - волновых структур
- самопересечение фронтов умеренно нелинейных волн. Самопересечение фронтов
приводит к различным последствиям у гамильтоновых (линейные волны и
солитоны) и диссипативных структур
(ударные волны, границы раздела фаз, автоволны )
Если в первом случае возможно
формирование особенностей, соответствующие катастрофам Тома - Арнольда [68]
(каустики), то во втором - может возникнуть новое явление. Фронт обобщенной
умеренно-нелинейной волны, рассматриваемый в первом приближении извне как
двумерная поверхность, может деформироваться таким образом, что в какой-то момент времени две различные точки границы
(обобщенной ударной волны) окажутся в одной точке пространства - происходит
слипание границ [73]
Разрыв твердых тел, радиоактивный распад
и слияние ядер атомов, образование капель, формирование брызг, появление
трещин, стягивание объёмов нефти при её откачке, землетрясения - представляют
собой физическую интерпретацию описанного выше процесса. Биологическими
интерпретациями того же явления могут служить слияние и деление клеток,
рождение нового организма. Примером проявления этого механизма в социальных процессах
может служить формирование и разрушение империй, слияние корпораций.
В
качестве одного из последствий такого совмещения в пространстве различных
частей границы можно предположить превращение точки соприкосновения в линию (в
двумерном случае) (рис.3.3)
Рис.3.3
Формирование вихревой ударной волны второго рода.
или поверхность - в трёхмерном,- сдвоенной границы.
Формирование сдвоенных границ и их перемещение в сплошной среде может
сопровождаться образованием вихревой ударной волны второго рода нулевого или
первого порядка в терминологии К.Трусделла - вихревой пелены.
В большинстве практически важных случаев
появление вихревых ударных волн первого рода сопровождается пересечением и
слипанием границ и фронтов и отделением сформировавшегося вихревого объема от
остальной части границы.
Гидродинамическими
примерами таких явлений можно считать обтекание крыла конечного размаха,
течение около плохо обтекаемых тел, обтекание ниш и отверстий, кавитационные
течения и т. д.
Процесс разрушения фронтов
умеренно-нелинейных волн может происходить и несколько иным способом. Этот
способ связан с множественным перезамыканием границ и появлением тел-волн малых
масштабов в районе разрушения.
Физическими
примерами таких явлений могут служить
а)
образование на поверхности разрушающихся волн брызговой струи, состоящей из
множества капель;
б)
образование пузырьковой кавитации на поверхности движущихся в жидкости тел при
высоких скоростях движения;
в)
формирование лавин, сходящих со склонов гор;
д)
формирование кучи песка.
Последний пример, в теоретическом исследовании
которого вновь, как и при исследовании многих других нелинейных явлений,
появились степенные функции, стал математической моделью для построения теории
самоорганизованной критичности, оказавшейся полезной моделью при исследовании
транспортно-информационных систем (см., например,[74]).
Можно высказать гипотезу, что явление
диссипации в макропроцессах является следствием формирования вихревых ударных
волн первого и второго рода на микроуровне и наноуровне. Аналогичная гипотеза
может быть высказана и о возможной
природе вязких потерь энергии при турбулентности.
3. Грибовидные
структуры.
Одним из возможных
следствий возникновения вихревых ударных волн первого и второго рода является
появление трехмерных структур, называемых в настоящее время грибовидными.
Характерным примером возникновения
вихревых ударных волн первого и второго
рода и формирования грибовидной структуры является процесс образования
циркуляционного течения около движущегося в жидкости крыла конечного размаха.
С изложенных выше позиций крыло может
рассматриваться как тело - волна, а его граница как обобщенная присоединенная к
телу нелинейная ударная волна, движение которой создает в жидкости поле
скоростей и давлений, перемещающихся относительно частиц жидкости со скоростью,
равной скорости движения тела.
Вблизи границы тела - волны наряду со
скачком плотности параметра, переносимого этой волной, обычно формируется также
волна резкого скачка касательных скоростей (вихревой пограничный слой). На
границе движущегося тела имеются, как минимум, две критические точки, т. е.
точки, в которых скорость жидкости в незавихренной области близка к скорости
движения тела, и наблюдаются максимальные продольные градиенты завихрённости.
Если провести вполне уместную аналогию с
фазовым пространством конечномерной динамической системы, то критические точки
около движущегося крыла во многом окажутся аналогичными седловым точкам
сепаратрисы фазового пространства. И так же, как вблизи седловых точек
сепаратрисы фазового пространства конечномерной динамической системы возможно
появление бифуркации рождения цикла [16, 75], вблизи критических точек потока
может сформироваться вихревая ударная волна первого рода, которая затем
отделяется от поверхности крыла, формируя вихревую пелену-вихревую ударную
волну второго рода. Автомодельным аналогом этого явления служит формирование
ревербератора при огибании препятствия автоволнами со скачком нормальных скоростей
[47]).
Появление вихревых ударных волн тем
более вероятно, чем ближе критическая точка к уже заданной самой формой профиля
крыла вихревой ударной волне первого рода в виде острой задней кромки с
заданным скачком наклона касательной к поверхности крыла.
Указанная аналогия может быть обоснована
следующими рассуждениями, которым можно придать строгую математическую форму
[76]. В частном случае изучения динамики человеческой популяции это было
сделано в нашей монографии [45].
Динамика сплошной
среды описывается, как минимум, двумя типами дифференциальных уравнений:
системой нелинейных уравнений в частных производных для определения зависимости
вектора скорости от координат пространства (уравнениями неразрывности,
сохранения количества движения и энергии), и системой обыкновенных
дифференциальных уравнений для определения траекторий частиц сплошной среды,
отражающих тот факт, что скорость есть производная от радиуса - вектора
траектории по времени. Если решение первой системы уравнений получено, то в результате
подстановки его во вторую систему получим систему обыкновенных дифференциальных
уравнений с размерностью, равной размерности пространства, фазовые траектории
которых есть траектории частиц сплошной среды. Это условие активно используется
в теории динамических систем. Однако, обычно характер фазового пространства
определяется заранее заданным типом правых частей обыкновенных дифференциальных
уравнений и получающиеся при этом фазовые потоки редко соответствуют каким-либо
реальным течениям сплошной среды. Можно поставить обратную задачу - строить и
классифицировать типы и особенности обыкновенных дифференциальных уравнений по
типам уравнений и особенностей динамики сплошной среды, которым они
соответствуют. Такой подход, во-первых, обосновывает частичное подобие
структур, формируемых в сплошной среде особенностям и аттракторам фазового
пространства стандартных динамических систем, а во-вторых позволяет
сопоставлять специфические структуры, формирующиеся в сплошной среде, например,
структуры, классификация которых приводится здесь, с особыми точками,
аттракторами и репеллерами фазового пространства систем специфических
(нестандартных) обыкновенных дифференциальных уравнений. Так, например, любому
обыкновенному дифференциальному уравнению первого порядка с одной переменой
путём комплексификации может быть сопоставлено некоторое течение идеальной
несжимаемой жидкости и наоборот, всякому течению идеальной жидкости могут быть
сопоставлены сначала одно комплексное. а
затем одно или два связанных дифференциальных уравнения [76].
Продолжим качественный анализ динамики
потока около крыла. Вблизи критических точек так же, как и вблизи точек слома
границы, наблюдаются максимальные продольные градиенты завихренности и
появляются условия для возникновения спиральных вихревых ударных волн первого
рода. Наиболее интенсивно этот процесс происходит вблизи критической точки,
расположенной около задней острой кромки крыла, около которой как сами величины
интенсивности завихрённости, так и её градиенты максимальны.
Утолщение пограничного слоя в этом
районе создает условия для формирования между задней кромкой крыла и
расположенной над ней критической точкой спиральной вихревой структуры -
вихревой ударной волны первого рода, математический анализ автомодельного
формирования которой выполнен в ряде работ (см. например, [77]). Диффузия
завихрённости и внутренние потери устойчивости вихревой поверхности приводят к
формированию вихревого пузыря. Взаимодействуя c потоком около крыла, вихревой
пузырь формирует течение, приводящее к самопересечению вихревых слоев и
образованию вихревой пелены - вихревой ударной волны второго рода,
возникновение и рост которой отделяет вихревой пузырь от крыла.
Рис.3.4
Формирование вихревых ударных волн первого и второго
рода при обтекании задней кромки крыла.
При этом вблизи боковых кромок крыла конечного размаха
вихревая пелена окаймляется постоянно формирующимися вихревыми ударными волнами
первого рода (концевыми вихрями). Возникает одна из форм пространственной
вихревой структуры, названная нами грибовидной.
Рис.3.5
Течение около крыла конечного размаха как нейтральная
грибовидная структура.
Возникшая структура достаточно сложна, так как включает
в себя вихревые ударные волны первого и второго рода, а также присоединенную к
движущемуся телу обобщенную ударную волну - границу тела. Элементы такой
грибовидной структуры движутся с существенно различными скоростями и вследствие
этого её продольный размер интенсивно растёт во времени.
Мгновенно
изменив угол атаки крыла до нуля, мы можем получить вихревое кольцо с
перемычкой, которое является одной из наиболее простых форм свободных
грибовидных структур (рис.3.6)
Рис. 3.6
Свободная нейтральная грибовидная структура.
Возникшая свободная грибовидная структура может
трансформироваться и тем самым влиять на движение окружающей её сплошной среды.
Рассмотренный
тип грибовидной структуры может быть назван нейтральным. Топологически возможны
грибовидные структуры еще двух типов. Грибовидные структуры
"женского" типа, представителями которых являются вязкие струи,
вытекающие из отверстий в среду, совпадающую со средой струи. В этом случае
происходит существенная трансформация вихревой пелены, которая, оставаясь
сдвоенной поверхностью, соединяется с обобщенной ударной волной (границей),
породившей грибовидную структуру. Вихревая пелена преобразуется в
"ножку" грибовидной структуры.
Рис.3.7
Грибовидная структура открытого типа.
В отличие от нее, например, струя
жидкости, вытекающая в воздух, представляет собой пример замкнутой
("мужской") грибовидной структуры, формирующейся на основании
имевшейся ранее границы раздела сред.
Рис.3.8.
Грибовидная структура замкнутого типа .
Наиболее характерным примером замкнутой
грибовидной структуры является осесимметричная картина отрывного обтекания
шара. Грибовидные структуры в
последние годы начали интенсивно изучаться
как экспериментально, так и теоретически [78]. Решения ряда вихревых и струйных задач гидродинамики
являются адекватными моделями для их описания.
Простейшим
примером гидродинамического, и не только гидродинамического, описания является
особенность типа концентрированного в точке диполя. Как следует из предыдущих рассуждений, эта
модель может также считаться характерной особенностью фазового пространства
соответствующего обыкновенного дифференциального уравнения, что позволяет включить вихревые и дипольные
особенности наряду с вихревыми ударными волнами в число основных сингулярностей
обыкновенных дифференциальных уравнений нестандартного типа.
В
двумерном случае грибовидная структура может быть приближённо смоделирована
парой равных симметрично расположенных концентрированных вихрей. Решение
подобной задачи, впервые полученное Кельвином, можно найти в любом учебнике по
гидродинамике. Если подойти к рассмотрению этого решения с позиций качественной
теории структур и бифуркаций фазового пространства обыкновенных
дифференциальных уравнений, то можно увидеть в ней характерные особенности,
являющиеся, по-видимому, особенностями всех грибовидных структур.
Можно
рассматривать две различные задачи.
1.
Свободное
движение вихрей, когда скорость их перемещения равна средней скорости движения идеальной
жидкости вблизи вихря.
2.
Вынужденное
движение вихрей, когда скорость перемещения «присоединённого вихря» задаётся.
Первая
задача является специфическим резонансным вариантом второй, при этом
резонансным условием является равенство задаваемой скорости перемещения пары
вихрей и среднего вектора скорости жидкости в районе их расположения. Это
условие является частным случаем обнаруженного нами класса явлений, который
может быть назван вихре - волновым и структурным резонансом .
Основным
безразмерным параметром, определяющим бифуркационные характеристики
рассматриваемой структуры при решении второй задачи, является отношение
циркуляции вихря к скорости движения вихревой пары (или скорости набегающего
потока) и к расстоянию между вихрями. При изменении этого параметра вид
замкнутой области, формируемой течением около вихрей, проходит несколько
качественных бифуркаций [79].
Этой
структуре соответствуют три присоединённые волны. Тело – волна, формируемая
сепаратрисой соответствующего гидродинамического течения, отделяющей внешнее
течение от внутреннего, максимальный
размер которого, измеренный в направлении движения, может быть принят за
длину волны, а скорость которого определяется скоростью перемещения системы вихрей.
Отсюда определяется частота этой волны.
Другой
волной является дипольная структура, амплитудой которой может считаться
интенсивность диполя, равная произведению циркуляции вихря на расстояние между
вихрями. Частотой этой волны можно считать отношение интенсивности вихря к
квадрату расстояния между вихрями, а длиной волны – само это расстояние.
Скорость волны может быть определена как циркуляция вихря, делённая на число 2
пи и расстояние между вихрями. В резонансном случае скорости обеих волн совпадают.
Эта простая модель может быть применена для описания грибовидных
структур всех типов.
Однако, реальные грибовидные структуры
обладают ещё одним свойством, не отражаемым рассмотренной выше схемой.
Это свойство наиболее характерно для
открытых грибовидных структур.
Оно состоит в обмене веществом с
окружающей средой, в наиболее общем случае проявляемом в захвате массы
окружающей среды, её переработке путем включения во внутренний циркуляционный
поток и возвращение ранее захваченной массы в окружающую среду. Простейшими
моделями такого движения являются модель идеального гидравлического движителя [80] и модель спутной струи за обтекаемым телом.[110]
Наиболее
широко распространены грибовидные и являющиеся результатом их трансформации
дипольные структуры в биологических и социальных объектах, где они принимают
различные специфические формы. Их длительное существование обеспечивается в
этом случае внутренней энергией активной
среды, в которой они формируются. По аналогии с автоволнами они могут быть названы
автогрибовидными структурами. Все живые существа и многие автономные органы
живых организмов можно отнести к грибовидным структурам.
Если
ещё раз обратиться к аналогии с обыкновенными дифференциальными уравнениями
обычного типа, то аналогами грибовидных структур в некоторой степени могут
считаться двумерные торы.
4. Возможные способы качественной трансформации
грибовидных структур.
Древовидные структуры.
Благодаря достаточной сложности
грибовидных структур может наблюдаться значительное разнообразие топологических
форм их трансформации, приводящие к бифуркационным изменениям этих структур.
Рассмотрим на качественном уровне
некоторые потенциально возможные типы трансформации грибовидных структур,
приводящие к их изменениям и появлению новых:
а) В первой
топологической форме (нейтральной) вихревая пелена благодаря вращательному
движению среды вокруг замкнутой вихревой ударной волны первого рода,
наматывается на неё и пополняет её завихрённость, а кроме того уходит по
нормали от вихревого объёма на
определённое расстояние, образуя переднюю границу свободно движущейся
грибовидной структуры. Эти два процесса приводят к тому, что асимптотически
вихревая пелена, уменьшая до нуля свою интенсивность, становится стационарной
поверхностью тока в системе координат, связанной с самодвижущейся структурой.
Грибовидная структура превращается в вихревой тор.
Наиболее интересным является случай,
когда внешний диаметр тора соизмерим с внутренним. В этом случае явно
проявляется дипольный характер грибовидных структур. Математическое описание
структур такого типа хорошо известно. Примером гидродинамической модели
трёхмерной вихревой кольцевой структуры, эквивалентной движущемуся в жидкости
диполю, является т.н. вихрь Хилла [81].(рис 3.9)
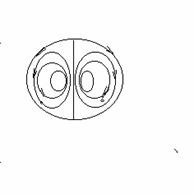
Рис. 3.9 .
Дипольная структура.
Вихрь Хилла .
Задача деформации и всплывания вихревого объёма в
стратифицированной жидкости решена в цикле работ И. М. Миндлина:
«Эта модель описывает эволюцию ограниченной однородной
тяжёлой жидкой массы в неограниченной однородной тяжёлой жидкой среде (жидкое
пятно в жидкой среде). Показано, что течение, начавшееся из состояния покоя
представляет собой эволюционирующий кольцевой вихрь типа грибовидного облака,
образующегося после мощного взрыва в атмосфере.» [82. С.9] .
б) Если в процессе трансформации вихревая пелена
подвергнется внешним возмущениям, то она, будучи обобщенной ударной волной,
может отреагировать на возмущение формированием вторичных поверхностных волн,
которые, в свою очередь, являясь существенно нелинейными, вновь формируют вихревые
ударные волны первого и второго рода и вторичные грибовидные структуры. Эти
вторичные вихревые и грибовидные структуры, хотя по своему происхождению
являются более сложными, так как сформировавшие их поверхности после
самопересечения становятся в некоторых случаях четырёхслойными, вследствие
перезамыкания и последующей диссипации могут потерять память о своем
происхождении и внешне выглядят как первичные грибовидные структуры или их
элементы. Этот процесс является одной из форм появления древовидных структур.
В
действительности процесс "забывания"- потери информации -
происходит практически на всех этапах формирования вихревых ударных волн и
грибовидных структур. Это связано с тем, что потеря устойчивости в виде
вихревых ударных волн первого рода происходит через спирализацию и
сформировавшиеся вихревые торы должны содержать в себе память не только о двух
или четырёхслойных поверхностях, но и об n-слойных поверхностях, с числом
слоёв, пропорциональном числу витков спирали, породившей вихревой тор. При
диссипации и многочисленных внутренних потерях устойчивости образовавшаяся вихревая или грибовидная структура,
фрактализуясь, увеличивая свою размерность на единицу, "забывает" о
своём происхождении.
(Здесь уместно отметить возможную аналогию между завихрённостью
и температурой. Динамика обеих величин
подчиняется уравнению типа уравнения теплопроводности. Следовательно, для
завихрённости можно ввести некоторый аналог энтропии. Само формирование
концентрированных вихрей - это энтропийный процесс, связанный с диссипацией
энергии. Однако, этот процесс значительно отличается от процесса перехода к
статическому равновесию, изучаемому в статистической физике, так как он
приводит не к "тепловой смерти", а к формированию новых вихревых и
грибовидных структур).
Формирование вихревых ударных волн
первого рода с последующей внутренней диссипацией завихрённости представляет
собой промежуточный процесс, приводящий в области формирования структуры к
максимуму "энтропии завихрённости", но не к максимуму энтропии в
термодинамическом смысле.
Гидродинамическим примером
множественного формирования вторичных вихревых и грибовидных структур такого
типа является турбулизация вихревой пелены за крылом или турбулизация границ струйного течения.
в)
Перезамыкание вихревых поверхностей двух грибовидных структур первого
топологического класса в зависимости от стороны перезамыкания может привести к
появлению квадрупольных структур двух типов (рис.3.10) квадрупольной структуры,
у которой пелена находится внутри торов и квадрупольной структуры, у которой
пелена находится вне торов и как бы охватывает их. Во втором случае возможно
сближение вихревых торов и формирование локального квадруполя.
Рис. 3.10
Квадрупольные структуры .
Если осуществляется перезамыкание двух
различных вихревых торов , то здесь также возможны два топологических варианта
.
3) Вариант 1
Если перезамыкающиеся торы представляют собой элементы
двух различных грибовидных структур, то слияние вихревых торов, по-видимому ,
автоматически приведёт к перезамыканию вихревых пелён , их соединяющих .
4) Вариант 2
Если торы представляют две части квадрупольной
структуры, то в результате перезамыкания квадрупольная структура может вновь
превратиться в дипольную .
е) В некоторых случаях
теоретически возможен "захват" вихревым
тором или закрученной "ножкой" грибовидной структуры элементов другой грибовидной структуры , что
может привести к установлению новых ближних связей и, возможно, к формированию
новых структур. Этот процесс открывает возможность установления иерархии
ближних связей между элементами грибовидных структур.
ё) В случае второго и третьего вариантов
грибовидных структур возможны иные
качественные формы их трансформации. Одной из них является винтовая спирализация
"ножки" грибовидной структуры как в случае отерытого -"женского
", так и в случае замкнутого-"мужского" вариантов.
Спирализация
может совпадать с формированием концентрированных вихревых структур (так
возникают кармановские дорожки за плохообтекаемыми телами и спиральные вихревые
следы за шарами )
Спирализация ножки "гриба"- это
фундаментальный процесс нарушения симметрии. Воронки на воде, смерчи и ураганы
- возможные примеры спирализации ножки “гриба”.
Закрутка ножки грибовидной структуры
может привести к появлению нового класса грибовидных структур - к структурам ,
названным нами клеточными . Это
может произойти в случае "разрыва"-
закрученной ножки грибовидной структуры (перезамыкания её границ) и
проникновения её внутрь вихревого тора . Так может возникнуть топологический
аналог биологической клетки.- грибовидная структура в виде "клетки со
спирально закрученным ядром."
"Клетка со спирально закрученным
ядром "- структура, динамика которой может быть исследована методами
современной математической физики Например, в качестве такой модели может быть
использован полый внутренний спиральный
вихрь, трансформирующийся во внешнюю дипольную оболочку (рис.20).
Рис.3.11.
Клеточная структура .
ж) Аналогия построенных вихре - волновых структур с
биологическими объектами подсказывает ещё три возможные формы трансформации
"мужских" и "женских" грибовидных структур -
1) формирование
на их "ножках " (по аналогии с вариантом а) новых , вторичных
грибовидных структур , как на материнских поверхностях. (рис.3.12)- частичное вегетативное размножение грибовидных
структур.
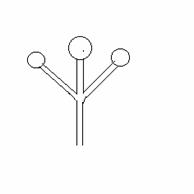
Рис. 3.12
Частичное “вегетативное” размножение грибовидных
структур .
2) Если на вихревой торе грибовидной структуры,
имевшем первоначально форму, близкую к
форме кругового тора, возникнут вследствие потери устойчивости стоячие волны,
которые затем развиваясь, и увеличивая свою амплитуду, разобьют шляпку
грибовидной структуры на ряд сегментов, то в случае аналогичного процесса в ножке гриба имеем
полное размножение структуры. Если же ножка гриба не расщепляется, то
получается новая разновидность грибовидной структуры, названная нами с
использованием биологической аналогии-"цветком" (рис.3. 13)
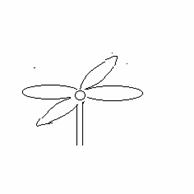
Рис.3.13
Формирование “цветка”
Квадрупольные структуры с пеленой, находящейся снаружи
от вихревого тора, могут вследствие потери устойчивости пелены сформировать
вместо одной охватывающей пелены множество внешних соединительных трубок Примерно так устроена кровеносная
система и некоторые другие
транспортно-информационные системы человека.
В большинстве случаев описанные процессы должны иметь
каскадный характер, приводящий к появлению множественности "шляпок"
или "ножек" или связанных
между собой грибовидных структур. Однако, в отличие от каскада бифуркаций
Фейгенбаума, вместо хаотического аттрактора, семейства грибовидных структур
трансформируются в новый тип структур, которые были названы нами древовидными.
Основным свойством древовидных структур является наличие связанных между собой
грибовидных структур или волновых структур более низкого уровня, генетически
происходящих друг от друга.
Древовидные структуры являются
переходными к принципиально новому
классу вихре - волновых систем, названному нами транспортно- информационными
системами.
5. Транспортно-информационные системы.
Транспортно-информационные системы
состоят обычно из большого числа связанных между собой, а иногда и произошедших
одна от другой грибовидных и древовидных структур или вихре - волновых структур
более низких классов. В случае, если все структуры абсолютно идентичны, могут
быть рассмотрены два предельных варианта .
Первый - структуры практически не
взаимодействуют между собой. В этом случае они эквивалентны идеальному газу,
поведение которого описывается методами кинетической теории. Динамика большого
числа таких структур почти не зависит от их внутреннего строения и при
рассмотрении большого ансамбля "частиц" - грибовидных структур,- их
динамика вновь описывается волновыми уравнениями. Спираль качественного анализа
вихре - волновых структур совершает полный оборот, и мы вновь, на ином
масштабном уровне приходим к линейным волнам .
По иному обстоит дело в случае, если
между структурами существуют те или иные связи. Из нашего рассмотрения можно
предположить существование между ними как минимум двух типов связей-
1) Полевых - дальних, связанных с тем , что структура
сформировалась в сплошной среде, является дипольной и взаимодействует с другими
структурами среды, создавая вокруг себя стационарное поле, либо посылая в среду
линейные волны, умеренно нелинейные волны, вихревые или грибовидные структуры.
2) Ближних связей - определяемых генетическим
происхождением грибовидных структур друг от друга. Они могут быть также связаны
с перезамыканием грибовидных структур или захватом одной грибовидной структурой
элементов другой и осуществляются,
например, путём транспорта массы, энергии и информации по ножке грибовидной
структуры .
3) Не исключён
и несколько иной (промежуточный) тип связи, состоящий в том, что некая
грибовидная структура порождает путём локального перезамыкания дочерние
структуры меньшего масштаба, которые затем захватываются другой грибовидной
структурой. Порождение и захват могут стать регулярными. Возможно также периодическое
перемещение элементов грибовидных структур или тел - волн между двумя
грибовидными структурами. Тем самым
возникают транспортные связи. То есть дочерние грибовидные структуры или
более простые элементы тел - волн транспортируются либо по специальным
транспортным магистралям (например, ножкам грибовидных структур) либо свободно
перемещаясь в пространстве.
Полевое
взаимодействие вихревых и грибовидных структур между собой а также с
порождёнными ими нелинейными волнами достаточно интенсивно исследуется в
настоящее время как экспериментально, так и теоретически с использованием
методов математической физики.
В последние
годы в этом направлении сделаны блестящие открытия. Так, например в
шестидесятые годы был открыт нелинейный
волновой резонанс при взаимодействии поверхностных и внутренних волн на границе
раздела сред различной плотности [83]. А в восьмидесятые годы одним из авторов
с группой сотрудников было обнаружено новое явление , возникающее при движении
несимметричных тел-волн в неоднородной слошной среде , названное ими вихре -
волновым и структурным
резонансом.[31,84].
Вихре - волновые резонансные процессы
являются одной из широко распространённых форм нелинейного взаимодействия волн
и вихрей, а новые формирующиеся резонансные
структуры могут оказаться особенно устойчивыми и обладающими качественно
новыми свойствами, отличными от свойств формирующих их структур. Отыскание в
природе резонансных структур такого рода и их детальное исследование
представляет собой перспективную научную проблему. Именно совокупность уже
открытых и ещё не открытых резонансов различных
типов, по нашему мнению , является одной из основных движущих сил
самоорганизации структур и систем.
Совершенно иного подхода требует
исследование "ближних" связей, так как именно они в основном
определяют те новые свойства, которыми обладают сложные транспортные системы.
Ближние связи позволяют отдельным грибовидным структурам направленно
обмениваться массой, энергией и информацией.
По-видимому, ближние связи практически
всегда осуществляются "квантами" , то есть дискретными порциями,
фактически такими порциями являются грибовидные структуры или их части, либо
простые тела-волны. При этом такие связи оказываются четко направленными.
Существование устойчивых транспортных направленных связей позволяет достаточно
простыми способами осуществлять математическое описание различных систем с
ближними связями. В основе этого описания лежат обычно методы теории графов и
сетей , интенсивно развивающиеся в последнее время.[85]-[88].
Примером математического анализа динамики простейшей
транспортной динамической системы является работа [89],
Несмотря на то, что четвёртый, пятый и
шестой классы волновых структур и систем встречаются и в неживой природе,
наиболее широко они распространены в технических, биологических и социальных
системах. Поэтому общие закономерности их динамики оказываются важными не
только для физики и химии, но и, главным образом, для технических приложений,
наук о Земле, биологии и наук о человеке и обществе.
Внутри
класса информационно-транспортных систем могут быть выделены подклассы,
различающиеся особенностями процессов, в которых участвуют входящие в них
элементы (кванты) и подсистемы.
а) Системы квази - детерминированного типа,
бифуркационные процессы внутри которых оказывают незначительное влияние на их
макропараметры. Основным свойством таких систем является значительная разница
между масштабами самой системы как обобщённой волны и отдельных элементов
(квантов), её составляющих, а также близость геометрических параметров квантов
и широкий спектр их энергетических уровней. Для их изучения существуют глубоко
разработанные методы равновесной и
неравновесной статистической физики, термодинамики и механики сплошных
сред. При этом квази-детерминированность на системном (обобщённо - волновом)
уровне допускает различную степень хаотичности на уровне квантов. Большинство
макроскопических объектов неживой природы относится к этому подклассу.
б) Транспортно - информационные системы, у которых
реализуется иерархическая материальная и информационная связь между уровнем
системы - волны и элемента – кванта. В таких
системах обычно выстраивается масштабная иерархия подсистем, каждая из которых
может обладать свойствами волновых структур классов более низкого уровня. Эта
масштабная иерархия имеет обычно квази - фрактальный характер. При этом общее
число квантов, входящих в систему, оказывается значительно больше, чем число
уровней иерархии. Именно в таких системах экспериментально наблюдается
соответствующее их квази - фрактальной структуре степенное статистическое
распределение масштабов элементов и подструктур. Отмечая главное свойство таких
систем, наличие связей между уровнями иерархии, которое называют целостностью,
Ю.К. Крылов назвал такие системы интаэросистемами, и предложил назвать науку,
их изучающую, интаэрологией [90-92]. Интаэрология Ю. К. Крылова может стать
одной из базовых составляющих синергетической методологии. В транспортно -
информационных системах в ряде случаев может существовать некоторая величина,
например, энергия, расход или объём, передаваемая с одного уровня иерархии на
другой без изменения, что также обеспечивает целостность системы. Это условие
является основанием для названия данного нами такого рода системам «идеальный
трансформер» [93].
Транспортно-
информационные системы, второго и более высоких подклассов могут быть
способными к размножению, то есть к формированию себе подобных систем.
Способность к размножению не является прерогативой только транспортно-
информационных систем. Практически в той или иной степени это свойство
характерно для любых колебательных и волновых систем, начиная от линейных
колебаний и волн. Однако, когда мы переходим к рассмотрению транспортно –
информационных систем второго и более высоких подклассов, то их размножение
может иметь специфический характер, проявляя, особенно у живых систем, такую
сложность, которую невозможно даже помыслить у структур более простых типов.
Здесь возникают структурно-волновые резонансы и могут появляться
логарифмические законы распределения параметров элементов. В последние годы
большое внимание уделяется исследованию в таких системах специфических форм
резонанснсных явлений, называемых гармоническими резонансами, родственными
цепочкам кратных резонансов в нелинейных колебательных системах. Формирование
резонансов такого типа осуществляется как каскадный процесс, передающий энергию
и информацию с одного уровня иерархии на другой. Анализ процессов такого типа
приводит в простейшем случае к геометрической прогрессии временных и
пространственных масштабов, а на следующих уровнях рассмотрения – к обобщённым
рядам Фиббоначи и теории ритмокаскадов.[1,49,93-102]
в. Транспортно- информационные системы, способные
моделировать свою динамику и динамику
окружающей среды – поля и выбирать близкие к оптимальным модели бифуркационного
поведения. Именно у таких систем интенсивно развивается, определяя их эволюцию,
внутренний контроллер, который назван нами гомеостатическим [41- 46].
г. Транспортно- информационные системы, обладающие
сознанием и творческими способностями.
Так как транспортно – информационные
системы обычно состоят из большого числа элементов, которые могут отличаться
как масштабами, так и другими параметрами, то при исследовании этих систем
существенную роль играют соответствующие статистические закономерности.
Эти закономерности должны быть
различными для
транспортно-информационных систем двух первых подклассов. Ввиду
сложности иерархической структуры систем второго и более высоких подклассов в
них могут встречаться и распределения параметров, свойственные для систем
других более низких подклассов. Этой проблеме в настоящее время посвящено
значительное количество работ, обзор которых дан в ряде статей и монографий (см., например, [90-93]). При
этом, в большинстве работ было показано, что если система находится в состоянии
статистического равновесия, то при возрастании количества элементов системы,
распределения элементов по их свойствам
оказываются со всё более возрастающей точностью удовлетворяющими нескольким
достаточно простым законам. Для систем первого типа это закон, описываемый
показательными функциями, приводящий к основным соотношениям равновесной
термодинамики, а для систем второго типа – это гиперболическая или более общая
степенная зависимость, имеющая очень много названий, так как она была
обнаружена в различных областях знаний.
Мы будем в дальнейшем придерживаться
терминологии [90-92] и называть это распределение распределением Ципфа -
Мандельброта. Существование подобной зависимости и её универсальность
свидетельствовали о том, что системы второго класса, куда относятся и многие
самоорганизующиеся системы, обладают некоторым своим универсальным свойством,
аналогичным второму закону термодинамики, которое заставляет эти системы
стремиться к некоторому состоянию, статистические свойства которого отличаются
от термодинамически - равновесных. Возникал также вопрос о связи закона Ципфа -
Мандельброта с экспоненциальными распределениями, характерными для систем
первого подкласса. Для решения этих проблем предлагались различные физические
модели.
Авторы,
например, обратили внимание на формальную аналогию между гиперболическим
статистическим распределением и параметрами потока от вихрей и источников, в
которых сохраняется расход и циркуляция, что позволило искать аналогии в
поведении таких систем с вихревыми и грибовидными (дипольными) структурами.
Кроме того, гиперболический закон изменения амплитуды колебаний и волн в
зависимости от частоты наблюдается при резонансных явлениях, что в некоторых
случаях, возможно, свидетельствует о резонансной природе возникновения
распределения Ципфа-Мандельброта.
Важной
проблемой является исследование нестационарных режимов, приводящих
асимптотически к гиперболическим и более общим степенным распределениям.
Прорывом в этом направлении оказалась теория самоорганизованной критичности,
которая вскрыла один из возможных механизмов выхода системы второго класса на
статистически равновесное для неё состояние со степенным законом распределения
[74 ].
Большой
вклад в исследования нетрадиционных, как их ранее называли, распределений
внесли Ю. К. Крылов и Б. И. Кудрин, исследовавшие многие математические особенности этих
распределений и получившие богатый эмпирический материал [90 - 92].
Однако
распределения Ципфа-Мандельброта имеют настолько всеобщий характер и возникают
в различных, системах и процессах: природные катастрофы, лесные пожары и
землетрясения, рыночная экономика и распределение числа слов в словаре и
тексте, количество книг и учёных, распределение видов в популяции и т.д. и
т.п., - что можно предположить, что должен существовать некий универсальный
закон природы, выражаемый самыми общими математическими формулами, не
зависящими от той интерпретации, которая будет ему дана. Попытка отыскания такого закона была сделана
Б.И. Кудриным и Ю.К. Крыловым, показавшими, что
степенному закону удовлетворяют распределения простых множителей набора
целых чисел, что ещё раз указало на универсальность этого закона распределения,
но не полностью решило проблему [92]. Ещё один, более близкий к динамике систем
подход, являющийся обобщением подходов Гиббса и Больцмана, был
предложен Ю.К. Крыловым [90]. По
его мнению, получение того или иного закона может быть осуществлено на пути,
начатом Больцманом при выводе экспоненциального закона распределения частот
встречи состояний молекул в зависимости энергии этих молекул. А именно,
отыскание такого распределения, которое даёт максимум числа разбиений множества
на классы при некоторых дополнительных ограничениях [90]. Путь, намеченный Ю.
К. Крыловым оказался наиболее плодотворным. На этом пути В. П. Маслову [103]
удалось доказать общую математическую теорему о свойствах множества отображений
элементов множества целых чисел 
, обладающих тем свойством, что их сумма постоянна и равна
заданному числу 
на совокупность 
упорядоченных
неотрицательных чисел 
при некотором
дополнительном условии относительно
заданного числа 
. Результатом этой теоремы явилась возможность обоснования распределения
Ципфа-Мандельброта и более общих законв распределения особенностей в
динамических системах.
Анализ динамики грибовидных структур и тел –волн
позволил предсказать возможность
появления принципиально нового типа взаимодействий, сущность которых состоит во
аномальном взаимодействи умеренно нелинейной
волны – границы, - как с внутренним объёмом, так и с внешней средой.
Качественный анализ такого нелинейного взаимодействия позволил обосновать
механизм возникновения нового явления –
вихре - волнового и структурного резонанса. Основными необходимыми условиями
возникновения открытого явления являются пространственная близость в течение
определённого промежутка времени взаимодействующих тел и (или) волновых картин,
равенство их масштабов и способность их к взаимодействию с полем, приводящая к
изменению некоторых основных свободных параметров взаимодействующих объектов.
Вихре -
волновой и структурный резонанс может явиться одним из главных механизмов
возникновения и стабилизации структур от нана- масштабов до масштабов
Вселенной.- то есть одной из причин структуро- и системо - формирования, в
частности, у биологических объектов и в социальных системах.
Характерным
примером цепочки таких структурно-волновых
резонансов является игра на инструменте виртуоза-скрипача. Жёстко
закреплённая струна представляет собой в первом приближении одномерную среду с
упругими свойствами, определяющими тип волнового уравнения и соответствующее дисперсионное соотношение.
Закрепление струны вводит в действие
структурно - волновое её взаимодействие с корпусом инструмента, представляющим
тело-волну. Это взаимодействие является резонансным, так как определяет
однозначно спектр длин допустимых стоячих волн, которые могут выжить в струне.
А дисперсионное соотношение, определяемое упругими свойствами струны, в свою
очередь однозначно определяет спектр частот колебания струны. Это первый
структурно – волновой резонанс, который достаточно просто описывается
математическими формулами и порождает то, что мы обычно называем собственными
колебаниями струны. Вторая стадия резонансного взаимодействия состоит в
непосредственном соприкосновении двух тел-волн – закреплённой струны и смычка.
Движение смычка относительно струны приводит к локальному перемещению и
количественному изменению сил, действующих на струну, и связанных с ними её
перемещений. Тем самым на волновую систему, представляющую собой закреплённую
струну воздействует другая волновая система (тело-волна)- смычок. Это
воздействие связано с изменением правой части уравнения, описывающего силовое
механическое взаимодействие. Воздействие смычка может быть представлено в виде
интеграла Фурье, из всего спектра которого за счёт резонанса выживают только те
гармоники, которые совпадают с собственными гармониками системы струна -
инструмент. Здесь второй раз действует структурно- волновой резонанс.
Колеблющаяся струна находится в поле - воздушной
сплошной среде. Характеристики этой сплошной среды также описываются
собственным волновым дифференциальным уравнением. Свойство воздушных звуковых
волн таково, что их скорость постоянна. Спектр допустимых звуковых волн
практически непрерывен. Волновое взаимодействие колеблющейся струны с воздушной
средой также является резонансным. Из всех возможных звуковых волн
резонансно возбуждаются лишь те, которые
имеют частоты, соответствующие частотам колебаний струны. Еще один резонанс не
только закрепляет резонансные частоты, но и передаёт их в другую среду,
обладающую новыми свойствами - свойствами передачи резонансной частоты на
большие расстояния с большой скоростью – скоростью звука. Далее может быть
включён ещё один резонатор, зрительный зал, представляющий ещё одно тело-волну,
который резонансно усиливает звуковые волны, заставляя их отражаться от границ,
размеры которых подобраны таким образом, чтобы возникал пространственный
волновой резонанс с размерами звуковых волн. Далее в действие вступает новый
структурно-волновой резонанс, между улиткой уха и звуковыми волнами. Улитка
представляет собой сложную спиральную струну, собственная частота колебаний
которой на различных участках спирали различна. Поэтому, с каждой звуковой
волной резонансно взаимодействует только один участок улитки. Механические
колебания улитки уха резонируют в электрическими импульсами колебаний нейронов,
которые передаются в мозг. Резонансное узнавание мелодии позволяет замкнуть
процесс исполнения музыкального произведения через человека – музыканта,
который управляет движением смычка таким образом, чтобы вся цепочка резонансов
замкнулась в виде приятной и знакомой мелодии.
Такой же
качественный волновой анализ цепочки резонансов может быть проведён и для
зрительного, и для обонятельного, и для вкусового, и для тактильного
восприятия.
Взаимодействие
тел-волн а также грибовидных структур с окружающей средой, основные
закономерности которого описываются в настоящее время наиболее полным образом
методами динамики сплошной среды, обладают некоторыми специфическим свойствами,
которые мы попытаемся описать словесно. Движение тела - волны в сплошной среде
(например, жидкости или газе) вызывает в среде формирование поля локальных
распределений давления, которое в случае равномерного перемещения тела движется
в виде стационарной присоединённой картины (в чём также можно увидеть
резонансный процесс, ведь скорость перемещения тела и скорость перемещения
картины давлений, им вызванной, имеют одинаковую величину). Тело как бы
извлекает из всех возможных полей давлений то, которое имеет ту же скорость
перемещения, что и само движущееся тело. Это одна из форм структурно-волнового
резонанса - резонанса по скорости. Однако, реальная структура потока
оказывается значительно более сложной. Наряду с волной давления тело формирует
движущуюся с той же скоростью волну, описывающую поле вызванных скоростей. При
этом в частном случае несжимаемой невязкой среды эти поля оказываются жёстко
связанными – поле давлении однозначно определяется полем скоростей и наоборот.
В других, более общих случаях, картины поля скоростей и поля давлений связаны
лишь частично. Если в сплошной среде имеются неоднородности или среда сжимаема,
то влияние этих аномалий приводит к необходимости рассмотрения дополнительных
дифференциальных уравнений в частных производных, в решениях которых
присутствуют только те волновые частоты, которые удовлетворяют этим уравнениям.
Тем самым резонанс между неоднородностями среды, которые можно в свою очередь
считать частным случаем умеренно-нелинейных волн, и самой сплошной средой
отбирает из всего спектра возможных волн те, которые удовлетворяют заданным ограничениям.
Дополнительное резонансное взаимодействие этих оставшихся волновых структур с
движущимися телами существенно меняет структуру волн давлений и скоростей,
присоединённых к движущемуся телу.
Глава IV. Вихре-
волновой и (или) структурный резонанс. История открытия.
1.
Нелинейные резонансы поверхностных и внутренних волн в стратифицированной
жидкости.
Исследованию волновых движений в
сплошной среде посвящена обширная литература, в том числе и большое количество
монографий (см., например,[10], [51], [105], [151-153], [156]). И хотя
первичный анализ линейных моделей волновых течений в неоднородных средах не
указывал прямо на наличие какого-либо резонансного взаимодействия возникающих
волн между собой, однако, в последние десятилетия рядом учёных было открыто и
широко исследовано резонансное взаимодействие нелинейных поверхностных и
внутренних гравитационных волновых движений. О. M. Филлипсом, М. Лонге-Хиггинсом, Д. Бенни, В. Е.
Захаровым, А. Б. Шабатом, Л. М. Бреховских и его группой, Дж. Уиземом и другими
исследователями был теоретически предсказан, а затем экспериментально
подтвержден и подробно изучен нелинейный волновой резонанс между поверхностными
и (или) внутренними волнами [105]. Им удалось обнаружить теоретически и
исследовать экспериментально условия возникновения волнового резонанса. Такими
условиями, справедливыми как для поверхностных, так и для внутренних волн,
явились следующие [105].
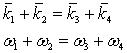
Здесь 
- волновые векторы и частоты двух взаимодействующих волновых
движений; 
- волновые векторы и частоты резонансных волн.
Более 20 лет тому назад одним из авторов
была высказана гипотеза о том, что аналогичные резонансные явления должны
возникать и при взаимодействии движущихся тел с диспергирующими волнами,
возникающими в сплошной среде.
2.
Результаты теоретических и экспериментальных исследований сил, действующих на
тела, движущиеся в ограниченном водоёме или обтекаемые ограниченным потоком.
Критические значения чисел Фруда по длине тела и глубине жидкости.
При равномерном поступательном движении
надводного судна или произвольного тела вблизи свободной поверхности воды с
постоянной скоростью ему сопутствует сложная волновая картина, которая в
системе координат, связанной с телом, остаётся неизменной.
Вот как описывается эта картина в [111].
«
При равномерном и прямолинейном движении судна форма свободной поверхности
представляет собой волновой рельеф, который движется одновременно с судном с
той же скоростью, что и у судна, и не изменяет своей конфигурации. Поскольку
основными волнообразующими центрами являются участки корпуса со значительной
кривизной поверхности, возникают две системы волн – носовая и кормовая. В
носовой и кормовой системах различают расходящиеся и поперечные волны.
Расходящиеся волны состоят из рядов сравнительно коротких, слегка вогнутых
гребней, располагающихся симметрично относительно ДП (диаметральной плоскости)
судна. Фронт каждой волны образует с ДП угол 
, величина которого на глубокой воде не изменяется при
изменении скорости судна. В зависимости от остроты носовой ветви ватерлинии
судна угол составляет 36-40 град.
Если соединить центры гребней расходящихся волн, то можно получить прямую,
составляющую с ДП угол, равный 0.5.»
Результаты многочисленных теоретических
и экспериментальных исследований волн, образующихся при движении судна на
глубокой воде при значениях чисел Фруда по длине судна 
, (где 
- длина судна в метрах), близких к 0.5,
позволили обнаружить специфическую картину взаимодействия судовых поперечных
волн, когда носовая волна усиливает кормовую и растет волновое сопротивление
судна. При этом половина длины поперечной волны, создаваемой движущимся судном,
оказывается равной длине судна. Однако это явление не рассматривалось ранее как
резонансное, в основном, вследствие отличия от общепринятого представления о резонансном взаимодействии
колебательной системы с внешним периодическим воздействием. Его теоретическое
исследование выполнялось с помощью линейной теории, результаты которой не
указывают прямо на резонансный характер взаимодействия. В данном случае ранее говорилось
лишь о благоприятной или неблагоприятной интерференции линейных волн, так как
никакого дополнительного усиления интенсивности источников, заменяющих судно, в
линейной модели, которая качественно описывала волновую картину и позволяла
приближённо рассчитывать волновое сопротивление, не учитывалось.
С уменьшением глубины водоёма значения 
, при которых наблюдается горб волнового сопротивления,
уменьшаются и стремятся к нулю при предельном мелководье, когда
становится малой
величиной (здесь 
- глубина водоёма). В предельном случае очень малых
относительных заглублений волновая картина определяется другим параметром -
числом Фруда по глубине погружения 
. В пределе при , стремящемся к нулю, наблюдается одна поперечная волна,
отходящая от носа судна, амплитуда которой становится максимальной при 
. При относительных скоростях, больших , поперечные волны исчезают, а волновое сопротивление резко
уменьшается. Аналогичные явления
наблюдаются и при обтекании препятствия. Вот что пишет Джеймс Лайтхилл,
описывая обтекание препятствия потоком
весомой жидкости [34. С. 319]:
«Мы опишем очевидно парадоксальный случай
волн, которые образуют совершенно стационарное течение. Во всех точках потока,
(включая и те, в которых находятся волны) течение является стационарным:
скорость жидкости не меняется со временем. Хотя подъём поверхности и может
локально обнаруживать правильное, почти синусоидальное изменение в
пространстве, он не обнаруживает никакого изменения во времени: гребни волн
всегда остаются на тех же местах при движении потока. Стационарная картина волн
порождается совершенно неподвижным препятствием в потоке. Это препятствие может
быть просто местной особенностью дна. В своём стихотворении «Ручей, текущий к
западу»[210] Роберт Фрост писал:
«Чернеющие воды, налетая
На затонувший камень, разбивались
И вспять бежали белою волной
Так белая на чёрных мчалась вечно,
Не наступая и не отступая…»
Постоянство потока поразило его воображение
«Волна та отражается от камня
С тех пор, как реки по земле текут»
Он увидел, что распространение гребня вверх по потоку
может в точности сводиться на нет течением вниз по потоку.
«Мы все перечим. Белою волной
Ручей течёт наперекор себе»
Он образно объяснил происхождение явления:
«Вот это устремленье вспять, к истоку,
Наперекор теченью, что несёт нас,
Есть дань теченья своему истоку.»»
Классические методы изучения взаимодействия
тел, движущихся в весомой жидкости, с волновыми системами, создаваемыми на
свободной поверхности, основанные на линейной теории волн, были разработаны еще
в конце прошлого века и интенсивно развивались вплоть до последнего времени, в
частности, применительно к исследованию судовых волн [106]- [111].
3.
Движение крыла вблизи границы раздела сред. Аномальные режимы обтекания.
Результаты теоретических исследований.
При движении вблизи свободной
поверхности или глиссировании несимметрично обтекаемого несущего тела, что
характерно для быстроходных судов, картина существенно меняется. Постановка и
общее решение такой задачи были выполнены в ряде классических работ, в
частности, в работах Н. Е. Кочина [108], М. В. Келдыша и М. А. Лаврентьева
[112] и Л. И. Седова [113]. Получение однозначного решения таких задач без
дополнительных допущений оказывается невозможным. При их постановке, как уже
отмечалось нами ранее, вводится дополнительное нелинейное условие на
поверхности крыла или глиссирующей поверхности - конечность скорости в районе
острой задней кромки (условие Жуковского – Чаплыгина - Кутта). Выполнение этого
граничного условия, сохраняя при линеаризации граничных условий на крыле и
свободной границе линейную зависимость характеристик потока от угла атаки,
приводит к нелинейной обратной связи между циркуляцией на поверхности крыла и
параметрами волновой системы, образующейся при его движении вблизи свободной
поверхности жидкости.
Численные расчеты гидродинамических
характеристик подводных крыльев выполнялись различными авторами первоначально
лишь для сравнительно больших глубин погружений крыла и предельных случаев
больших или очень малых значений числа Фруда по хорде крыла 
[114-120]. Это было связано с практическими
потребностями - суда на подводных крыльях имеют основной режим движения,
соответствующий большим значениям числа Фруда.
Попытки выполнения расчетов при малых погружениях и произвольных
значениях чисел Фруда приводили к значительным математическим трудностям,
связанным с необходимостью вычисления сложных волновых интегралов и решением
сингулярных интегральных уравнений теории крыла. Часть этих трудностей была
преодолена в конце пятидесятых, в начале шестидесятых годов, когда А.Б.
Лукашевичем [121], А. Н. Панченковым [122], Т.Нишиямой [123] , В. Исаи [124] и
др. в дополнение к данным М.В. Келдыша и М.А. Лаврентьева были выполнены
отдельные расчеты гидродинамических характеристик крыла, движущегося вблизи
поверхности весомой жидкости. Обобщение этих результатов было представлено в
монографиях [121, 125].
Однако, выполнить расчеты
гидродинамических характеристик подводного крыла во всем диапазоне чисел Фруда
и относительных глубин погружения не удавалось долгое время ни одному из
специалистов. Лишь в конце 70-х, начале
80-х годов подобные расчеты были
выполнены в США [126] при отработке численных методов решения нелинейных
волновых задач. Был обнаружен диапазон параметров потока, при котором
нелинейные численные методы не дают сходящегося решения. Экспериментальные
данные о волнах при буксировке
подводного крыла были получены Дж.Дунканом [140]
В 1982 году
на организованной М. А. Басиным и Ю. И. Фаддеевым конференции: “Гидродинамика подводного крыла
и глиссирующих поверхностей” М. А. Басиным [127], А. Я. Ткачом [128], М. А.
Макасеевым [129], М. В. Лотфуллиным [130], А. Н. Лордкипанидзе [131] были
сделаны доклады по результатам новых теоретических и экспериментальных
исследований гидродинамических характеристик крыла, движущегося вблизи
свободной поверхности весомой жидкости. (Эти исследования были заказаны
организаторами конференции). Результаты выполненных расчётов показали
существование диапазона значений чисел Фруда и относительных глубин погружения
крыла, при котором наблюдается аномальное поведение гидродинамических
характеристик крыла. В дальнейшем М. А. Басин, А. Н. Лордкипанидзе и А.Я. Ткач
[132-134], [169-174], усовершенствовав расчетные схемы с использованием
квадратурных формул Корнейчук –Мишкевича -Гур-Mильнера [135-137], провели в рамках линейной теории
систематические расчетные исследования по изучению влияния числа Фруда,
относительного заглубления, угла атаки, формы и толщины профиля, а также
удлинения крыла на его суммарные и распределенные гидродинамические
характеристики при движении вблизи свободной поверхности воды. Позднее аналогичные
расчеты по линейной и нелинейной теории,
были выполнены М. В. Лотфуллиным C. И.
Филипповым [138] B. Г. Щигуновым [139]. и другими
исследователями
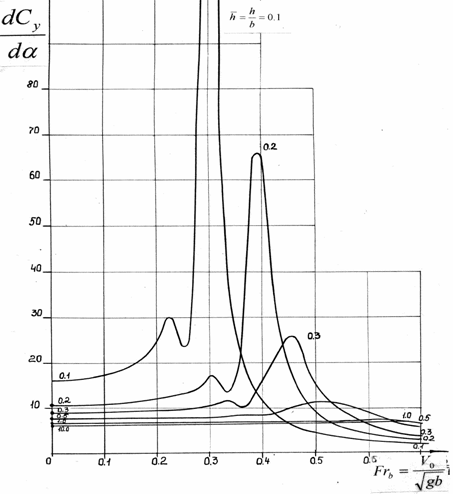
Рис 4.1. Расчетные графики зависимости производной от
коэффициента подъемной силы по углу атаки 
в функции от числа Фруда по хорде крыла 
для тонкого профиля, движущегося под свободной поверхностью
весомой жидкости при различных относительных заглублениях
(результаты расчетов по линейной теории ).
На рис. 4.1 представлены результаты расчётов по
линейной теории зависимости производной от коэффициента подъемной силы по углу
атаки 
в функции от числа Фруда по хорде крыла для тонкого профиля,
движущегося под свободной поверхностью весомой жидкости при различных
относительных заглублениях.
Как показали результаты расчетов, при
приближении крыла к свободной поверхности воды, начиная с 
, при определенном для каждого из относительных заглублений
числе Фруда по хорде крыла, уменьшающемся при уменьшении глубины погружения,
наблюдается интенсивный рост производной 
(где 
- коэффициент подъемной силы крыла, 
- подъемная сила крыла, 
- плотность жидкости, 
- площадь крыла в плане).
Так, например, при относительном
заглублении 
=0.2 и значении числа Фруда по хорде 
линейная теория предсказывает более чем
десятикратный рост по сравнению со случаем безграничной жидкости. С уменьшением
относительного заглубления теоретическое значение максимума кривой зависимости от резко увеличивается и даже стремится к
бесконечности при 
. Теория предсказывает существование режима с обострением
[48].
Представляет интерес зависимость от комбинированного числа Фруда, сформированного по площади
жидкости над крылом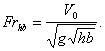 
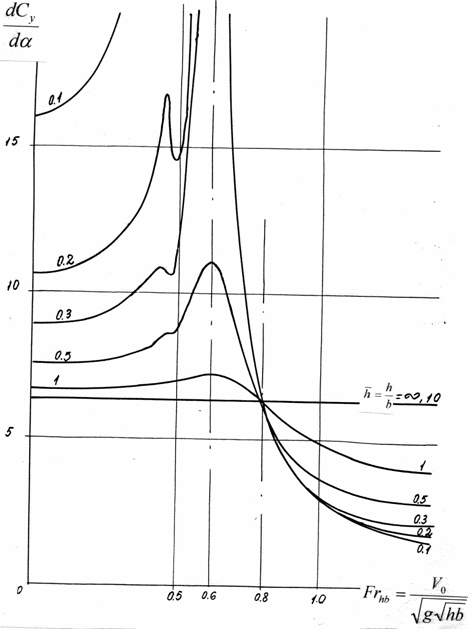
Рис.4.2. Расчетные графики зависимости производной от
коэффициента подъёмной силы по углу атаки в функции от числа Фруда по хорде и заглублению крыла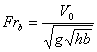 
для тонкого профиля, движущегося под свободной поверхностью
весомой жидкости при различных относительных заглублениях (результаты расчетов
по линейной теории )
Положение пика 
в широком диапазоне значений ,
практически не изменяется и соответствует величине 
. При значении 
заглубление
практически не влияет на подъёмную силу плоской пластинки (все кривые
зависимости в функции от 
пересекаются
практически в одной точке при значении
)
Уменьшение удлинения крыла приводит к
уменьшению величин резонансных пиков, однако, значения чисел Фруда,
соответствующих наступлению аномального роста значения при этом практически
не изменяются.
С уменьшением относительной глубины
погружения значение числа Фруда по хорде, соответствующее аномальному режиму,
уменьшается и стремится к нулю при очень малых заглублениях, тогда как число
Фруда по глубине погружения- 
растёт и стремится к
1. Аналогичные аномальные изменения силового воздействия на искривленные крылья (при несколько больших
значениях чисел Фруда) были обнаружены в результате расчетов зависимости угла
нулевой подъемной силы, определяемой кривизной профиля, от числа Фруда и относительной
глубины погружения (рис.4.3). Если в диапазоне чисел Фруда от единицы до бесконечности для тонкого
профиля в виде дуги круга угол нулевой подъемной силы практически не меняется и
имеет отрицательную величину, приближенно равную в радианах 
, где 
- максимальная относительная стрелка погиби дужки, то в
диапазоне чисел Фруда от 0.4 до 0.8 наблюдается резкий рост угла нулевой
подъемной силы, который при 
становится
положительным.
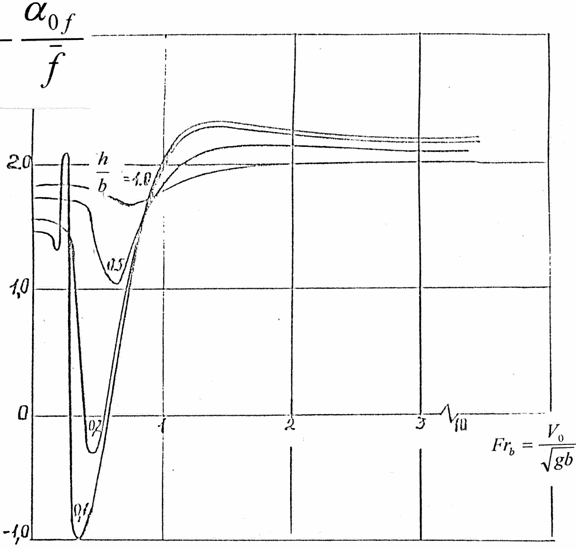
Рис. 4.3. Расчетные графики зависимости отношения угла
нулевой подъемной силы
(в радианах) тонкой
параболической дужки, движущейся под свободной поверхностью весомой жидкости к
её максимальной стрелке погиби 
в функции от числа Фруда по хорде при различных относительных заглублениях (результаты расчетов
по линейной теории).
Линейная теория, таким образом,
предсказывала парадоксальный результат. У тонкого профиля, имеющего форму
выпуклой по направлению к свободной поверхности дужки, при и 
должна
возникать не подъёмная, как обычно, а значительная топящая сила.
Еще более необычный аномальный эффект
предсказали результаты расчётов по линейной теории у крыльев с телесным профилем,
имеющим относительную толщину 
.
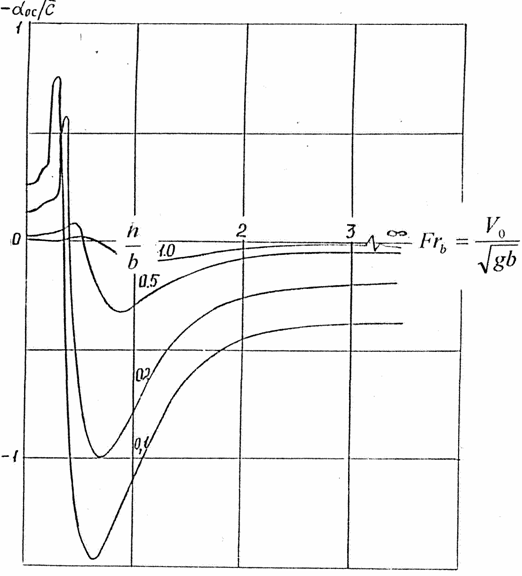
Рис. 4.4.Расчетные графики зависимости
отношения угла нулевой подъемной силы
(в радианах) тонкого
симметричного профиля, движущегося под свободной поверхностью весомой жидкости,
к его максимальной относительной толщине 
в функции от числа Фруда по хорде при различных относительных заглублениях (результаты расчетов
по линейной теории ).
У симметричных профилей крыльев при
попадании в аномальный режим также обнаружено теоретически резкое изменение
угла нулевой подъемной силы, который при незначительном увеличении числа Фруда
совершает зигзагообразный скачок от большого отрицательного значения до еще
большего (примерно в 2 раза) положительного значения.
Эти теоретические результаты, во-первых,
должны были получить соответствующее физическое объяснение, а, во вторых,
требовали экспериментальной проверки. Хотя имевшиеся разрозненные экспериментальные
данные [126], [127], [131], [140] качественно подтверждали существование
аномальных эффектов, однако, до выполнения систематических расчетов подробный
анализ этого режима не проводился.
С целью отыскания теоретического
объяснения полученных результатов были выполнены расчеты распределения давлений
по поверхности крыла в этом режиме и созданы дополнительные подпрограммы
расчета деформации свободной поверхности воды вблизи крыла. Результаты
последних приведены на рис.4.5.
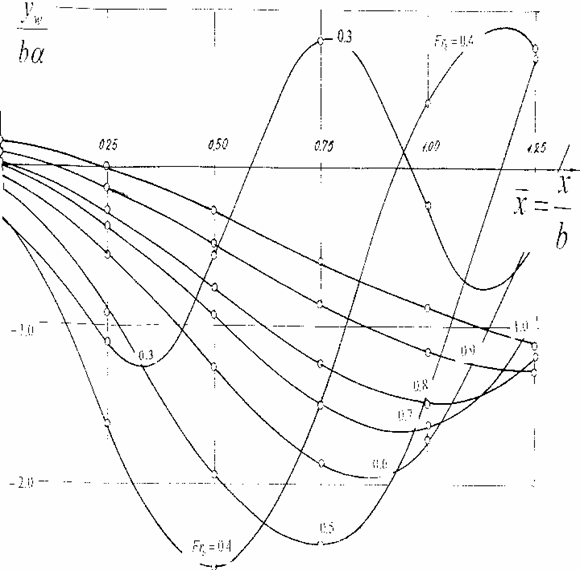
Рис.4.5. Результаты расчетов
относительной деформации свободной поверхности весомой жидкости 
над тонкой плоской пластиной, обтекаемой под углом атаки 
в зависимости от числа
Фруда по хорде крыла при относительном заглублении
= 0.2 (результаты расчетов по линейной теории ).
Эти расчеты показали, что главным
критерием, определяющим условие максимального теоретического значения величины , является совпадение определенной части длины сопутствующей
волны, формирующейся на свободной поверхности, с хордой крыла. При этом для
максимального воздействия на различные составляющие подъёмной силы эта часть
длины волны может оказаться различной, что несколько сдвигает по числам Фруда пики
воздействия на и на угол нулевой
подъемной силы 
.
Аномальные явления, приводящие к усилению степени гидродинамического
взаимодействия несущих тел и окружающей среды, однако, значительно менее
интенсивные, предсказаны теоретически и наблюдались в процессе эксперимента при
движении крыла вблизи твёрдого экрана. В этом случае, соответствующем на рис
4.1 стремлению к нулю числа Фруда по хорде крыла, также был обнаружен
теоретически и экспериментально подтверждён эффект, связанный со значительным
ростом подъёмной силы крыла и уменьшением сопротивления при приближении к
экрану. Рост аэродинамического качества в этом режиме движения был использован
при создании быстроходных судов и аппаратов. [121]
4.Кавитационное
обтекание крыла. Аномалии переходного режима.
Ещё одним явлением, при изучении
которого было обнаружено аномальное поведение потока около крыла, явился
переходный режим кавитационного обтекания подводных несущих поверхностей,
выступающих частей и лопастей гребных винтов быстроходных судов.
Развитие кавитационных явлений на поверхности
крыла начинается при критическом числе кавитации потока. которое приближённо
определяется как величина, близкая к максимальному коэффициенту разрежения на
поверхности крыла или в некоторой области течения вблизи крыла (вихревая
кавитация) [121].
Можно условно выделить три основных
режима кавитации профиля крыла при углах
атаки, близких к расчётным:
Режим частичной кавитации, когда
кавитационные явления наблюдаются в зоне длиной, не превышающей 0.6 - 0.7 хорды
крыла (плавный характер обтекания задней кромки в этом режиме практически не
нарушается);
Переходный режим, когда район замыкания
хвостовой части каверны находится в непосредственной близости от задней кромки
крыла. Нестационарный автоколебательный характер течения проявляется при этом
наиболее сильно и приводит к резкому, близкому к периодическому изменению сил
со временем.
Режим развитой кавитации, когда
хвостовая часть каверны находится на значительном (более полухорды) расстоянии
от задней кромки крыла и нестационарность в районе её замыкания сказывается на
силах в значительно в меньшей степени, чем при втором режиме.
Характер развития кавитации в каждом из
указанных режимов зависит от формы профиля крыла, его удлинения и, в
значительной мере, от угла атаки крыла.
Частичная кавитация наблюдается в двух
формах: пузырьковой и плёночной, или присоединённой. Первая форма кавитации
развивается при малых, так называемых безударных углах атаки, значения которых
(в радианах) не превосходят относительной толщины профиля. В этом диапазоне
углов атаки эпюра разрежений на засасывающей поверхности подводного крыла
близка к равномерной.
Область кавитации представляет собой не
сплошную полость, а скопление интенсивно растущих, а затем схлопывающихся
пузырей, заполненных парами воды или смесью паров воды и воздуха. Расширение и
схлопывание пузырей происходит в пределах хорды крыла. Согласно гипотезе А.Н.
Иванова влияние этой формы кавитации на
осреднённые во времени гидродинамические характеристики крыла эквивалентно
влиянию стационарной зоны постоянного давления, равного давлению насыщенных
паров воды 
при данной
температуре. Использование этой гипотезы позволяет при теоретическом
исследовании заменить зону пузырьковой кавитации эквивалентной присоединённой
каверной [121 ,199].
При увеличении угла атаки крыла
наступает момент, когда коэффициент разрежения в районе носовой кромки профиля
превышает его значение в районе максимальной относительной толщины. Вследствие
изменения распределения давлений вблизи носовой кромки профиля возникает единая
присоединённая каверна, в хвостовой части которой течение нестационарное.
Аналогично развивается частичная кавитация при отрицательных углах атаки, когда
в районе носовой кромки профиля на нагнетающей поверхности крыла возникает пик
разрежения.
Экспериментальные исследования показали,
что, пока длина присоединённой каверны не превысит 0.6 - 0.7 хорды, изменения
подъёмной силы вследствие нестационарного характера течения в её хвостовой
части малы по сравнению со средней величиной подъёмной силы, действующей на
крыло, и ими можно пренебречь. Это позволяет при теоретическом решении задачи о
крыле с частичной присоединённой каверной считать течение стационарным и
исследовать его с помощью методов установившихся струйных течений идеальной
жидкости. В некоторых случаях на засасывающей поверхности крыла
развивается система присоединённых
каверн малого удлинения, начинающихся в районе носовой кромки крыла. Участки
поверхности крыла между этими кавернами свободны от кавитации. Следует
отметить, что характер развития частичной кавитации и её формы (пузырьковая,
присоединённая или система присоединённых каверн малого удлинения ) в основном
определяются формой носовой кромки профиля и углом атаки крыла и связанными с
ними эпюрами распределения давлений. Иногда на крыле одновременно наблюдаются
различные формы частичной кавитации. Например, при малых отрицательных углах
атаки крыла сегментного профиля 
на его нижней стороне
развивается присоединённая форма кавитации, а на верхней, в районе максимальной
относительной толщины профиля, - пузырьковая.
При углах
атаки крыла, превышающих критические, наблюдается вихревая кавитация внутри
зоны оторвавшегося пограничного слоя, возникающая не на самой поверхности
крыла, а на некотором расстоянии от него.
Исследования
кавитационных течений при движении тел в жидкости, выполненные рядом авторов
[121, 175-178, 185-201], позволили теоретически решить в рамках стационарной
теории струй невязкой жидкости большое количество проблем, связанных с этим
разделом гидродинамики. В работах А.Н.
Иванова [185, 186, 199], М. П. Тулина [187-188], Дж. Гюрста [189], Р. Вейда
[190], А. Г. Терентьева [191], М. А. Басина [111, 121, 175-178,193], И.Т.
Егорова [175], М.А. Баевой и Л.П. Зилиста [121,178], A. В. Шалларя
[121,176,177, 192, 193], Б.В. Косова [192] И.Г, Шапошникова [121-178] и других
исследователей показано теоретически, что при кавитационном обтекании крыла в
режиме, когда длина каверны оказывается близкой к хорде как результаты
нелинейной теории струй идеальной жидкости, так и квазилинейной теории
указывают на существование аномальных параметров каверны и сил, действующих на
крыло.
Экспериментальные
исследования колебаний каверны, выполнявшиеся Кнэппом [194], а также В.П.
Ильиным и Ю. Л. Левковским [195, 196] и другими исследователями показали, что
при приближении длины каверны к длине хорды крыла амплитуда этих колебаний
интенсивно растет и частота их уменьшается. Силовые измерения в этом режиме кавитации
проводились различными авторами : О. Вальхнером[197], Нумахи [198], А.Н.
Ивановым [199], М.Мейером [200] а также И. Т. Егоровым, М. А. Басиным, Ю.М.
Садовниковым, А. В. Шалларем, Б. В. Косовым , Е.Б. Ануфриевым ,
И.Г.Шапошниковым и другими авторами [176-178, 192-193.207-209, 121].
Было
показано, что в этом режиме, во-первых, происходит резкое увеличение сил,
действующих на крыло, и толщины формирующейся каверны, а во-вторых, развиваются
интенсивные колебания каверны и циркуляции скорости вокруг крыла. Однако, в
этих работах не указывалось на резонансный характер этого режима обтекания и не
была дана физическая схема, описывающая причину резонанса и позволяющая описать
нелинейные вихревые структуры, формирующиеся при возникновении этого режима. Отметим,
что так же, как и в случае движения крыла вблизи свободной поверхности весомой
жидкости, решение квазилинейной задачи здесь может быть представлено в виде
системы линейных интегральных уравнений относительно двух функций - вихревой
интенсивности, распределенной по поверхности крыла и каверны, и распределения
источников, интенсивность которых характеризует распределение толщин профиля и
каверны.
Как и в
случае крыла, движущегося вблизи свободной поверхности воды, эта система имеет
бесконечное множество сингулярных решений для распределения источников и
вихрей, при выборе одного из которых используется два дополнительных условия: условие
Жуковского – Чаплыгина - Кутта для вихрей
и условие замыкания - для каверны. Именно эти два условия определяют нелинейную
взаимную связь между обеими искомыми функциями, одна из которых характеризует
относительную толщину каверны, а другая - распределение циркуляции по крылу и
его подъемную силу. Из рассмотрения аналитического и численного решения этой
задачи следует, что, когда длина каверны приближается к хорде крыла, происходит
утолщение каверны, приводящее к увеличению погиби средней линии системы
профиль-каверна, что, в свою очередь, увеличивает циркуляцию вокруг этой
системы и вновь утолщает каверну. Если рассмотреть теоретическое решение
стационарной линейной задачи в случае, когда длина каверны в точности равна
хорде крыла, то взаимное усиление приводит в линейной постановке задачи при
заданном малом угле атаки к неограниченному росту толщины каверны и коэффициента
подъемной силы крыла. Расчёты каверны в этом случае, выполнены М.А. Баевой
[121]. Решение соответствующей
нелинейной задачи, хотя и не дает бесконечных величин толщины каверны и
коэффициента подъемной силы, но указывает на существенный рост обоих указанных
параметров.
Удивительным
является тот факт, что даже при нулевом угле атаки пластины теоретически
существует такое нелинейное циркуляционное течение, когда около пластинки
возникает присоединённая каверна, плавно замыкающаяся на задней кромке крыла.
Подробный теоретический анализ такого течения выполнен М. А. Басиным и А. В.
Баландиным [31].
Таким
образом, анализ квазилинейной задачи, так же как и для крыла, движущегося
вблизи границы раздела сред, указывал в случае переходного режима кавитации на
те же признаки, которые были обнаружены ранее при исследовании
гидродинамических характеристик крыла, движущегося вблизи свободной границы.
5. Рождение концепции
вихре-волнового
и структурного резонанса.
Результаты анализа перечисленных выше
явлений показали, что аномальные режимы несимметричного обтекания тел
наблюдаются в случае сравнительно узкого диапазона изменения безразмерных
управляющих параметров, например, числа Фруда или числа кавитации. При этом в
критическом режиме оказываются близкими некоторые геометрические характеристики
потока: длина судна и половина длины поперечной присоединённой волны, хорда
крыла и длина полуволны, формирующейся на её поверхности, хорда крыла и длина
присоединённой каверны. Исключением, казалось бы, был режим движения крыла
вблизи экрана. Однако решение соответствующей аэродинамической задачи указывало
на то, что влияние экрана на аэродинамические характеристики крыла эквивалентно
влиянию симметрично расположенного относительно экрана крыла той же
геометрической формы. И здесь аномальное течение возникает как результат
взаимодействия двух симметрично расположенных крыльев, имеющих одинаковые
размеры.
Эти результаты указывали на возможную
аналогию с интенсивно изучавшимися в этот период волновыми резонансами. Была высказана гипотеза о том, что все указанные
явления имеют резонансную природу. Предполагалось, что резонансы этого типа
могут возникать при взаимодействии между основным потоком, формируемым при
движении тел в неоднородной среде, и диспергирующими внутренними волнами, а
также другими типами волновых и вихревых движений.
В
процессе обоснования предложенной гипотезы была создана единая классификация
волновых движений, вихрей, грибовидных (дипольных) структур и транспортно -
информационных систем, основанная на их волновой природе и отражающая бифуркационные процессы перехода
структур и систем одного более низкого класса в другой. Решён ряд модельных
задач взаимодействия тела с вихрями и волнами в резонансном режиме. Проведены
дополнительные экспериментальные исследования, позволившие определить
особенности аномальных явлений, возникающих при резонансном взаимодействии
движущихся тел с окружающей средой. Результаты этих исследований были
опубликованы в ряде статей и монографий [38-41, 157-179]. В настоящее время разрабатываются математические
модели, позволяющие определить общие условия возникновения вихре - волнового и
структурного резонанса при движении твёрдых тел и деформируемых объектов в
сплошной среде .
Для того, чтобы провести аналогию с
открытыми ранее волновыми резонансами, необходимым оказалось расширить
представление о волновых движениях, связанных с перемещением твердых тел в
жидкостях, проанализировать с новых позиций формирование циркуляции на
поверхности крыла и вывести на основе этих результатов критерии резонансного
взаимодействия тел с линейными и нелинейными волнами, возникающими в сплошной
среде.
Амплитуда волн, формирующихся около
крыла, движущегося вблизи свободной поверхности весомой жидкости в аномальном
режиме, даже при достаточно малых величинах углов атаки, относительной кривизны
профиля и относительной толщины крыла, рассчитанная в соответствии с линейной
теорией, оказывается выше предельных нелинейных волн. Попытки расчёта
нелинейных волн для этого режима численными методами, выполненные американскими
авторами [126], а затем В. Г. Щигуновым [139], показали, что существующие
методы решения нелинейных задач не дают устойчивой картины течения, то есть
появляются разрушающиеся волны. Отсутствие аналитических и численных методов
полного расчёта параметров обнаруженного режима течения предопределило
необходимость дополнения расчётных методов непосредственного решения задач
качественными методами анализа как физических причин самого резонансного
явления, так и его нелинейных последствий. Тем более, что предварительные
экспериментальные исследования обтекания крыла в обнаруженном режиме показали,
что при взаимодействии крыла со свободной поверхностью формируются
отсутствовавшие при других режимах вихре - волновые структуры, изучение которых
требует специальных методов исследования.
В последние годы интенсивно развиваются
новые качественные методы исследования нелинейных динамических систем и
волновых процессов. Проанализирована связь между ударными и солитонными волнами,
автоволнами, диссипативными структурами и режимами с обострением и обычными
линейными волновыми явлениями. Возникла новая наука, синергетика, изучающая
условия самоорганизации нелинейных систем (см., например, [8, 181,184].)
Осуществлённая нами в рамках
синергетических исследований классификации волн, вихревых, грибовидных и
древовидных структур, а также транспортно-информационных систем [31], [40-46]
позволила рассматривать движение твердого тела в жидкости как особую форму
нелинейной поверхностной уединенной волны, перемещающейся относительно частиц
жидкости со скоростью, равной скорости движения тела.
Основным геометрическим параметром этой
нелинейной волны является габаритный размер тела в направлении перемещения.
Особенность рассматриваемой волны состоит в том, что вблизи границы твердого
тела наряду с полем скоростей и давлений формируется также область
завихренности, образующая при определённых условиях тонкий пограничный слой.
Одновременно в сплошной среде, в которой
движется тело, существуют условия для
возникновения собственных, присущих данной среде волновых движений. Параметры
этих волн удовлетворяют обычно некоторым дифференциальным уравнениям в частных
производных. Воздействие движущегося твёрдого тела на такую среду эквивалентно
введению некоторых распределённых волнообразующих особенностей, Как было
отмечено выше, при постоянной поступательной скорости движения около тела
формируется практически неизменная волновая картина, перемещающаяся со
скоростью его движения. Формирование такой картины носит резонансный характер.
Движущееся тело резонансно стимулирует отбор из всего множества возможных
свободных волн такой их совокупности, которая может перемещаться, не меняя
своей структуры со скоростью движения тела. Аналогичное явление наблюдается при
натекании потока на препятствие. Эти явления многократно наблюдались и ранее и
условие равенства скоростей движения тела и присоединённых к нему волновых
картин существенно использовались для эффективного решения прикладных задач,
однако мало внимания обращалось на резонансный характер этого процесса. Этот
относительно простой тип структурно – волнового резонанса назван нами
резонансом по скорости.
Однако амплитудные характеристики
волновых картин, резонансно присоединённых к движущемуся телу, и связанное с
ними волновое взаимодействие, как показывают расчётные и экспериментальные
данные, существенно зависят при одной и той же скорости движения от габаритного
размера движущегося тела в направлении его движения. Когда этот размер
становится соизмеримым с размерами присоединённой волновой картины, наблюдается
рост амплитуды этой волновой картины и резко изменяется характер взаимодействия
тела и сплошной среды. Мы назвали этот процесс структурно - волновым резонансом
по скорости и длине волны. С наших современных позиций и это явление может
рассматриваться как резонансное, так как усиление интенсивности волн, вызванных
движением тела, в данном случае также носит
характер волнового резонанса. При постоянной скорости движения тело захватывает с собой волну (или спектр
волн заданной формы) с длиной, однозначно определённой скоростью движения тела
-возникает резонанс по скорости. При этом амплитуда захваченной волны
пропорциональна коэффициенту Фурье в интеграле Фурье, которым может быть
представлено граничное условие на поверхности тела. Этот коэффициент
максимален, когда длина тела близка к длине резонансно захваченной телом волны
[34, 142,182]. Тем самым, вследствие двойного резонанса по скорости и длине
волны при поступательном движении тела наблюдается более интенсивное
волнообразование и максимальные значения сопротивления движению тела.
Существенно меняется интенсивность
резонансного взаимодействия при движении в сплошной среде несимметрично
обтекаемых тел – крыльев.
Вблизи границ стационарно движущегося
твердого тела в связанной с телом системе координат обычно имеются, как
минимум, две так называемые “критические точки” (седловые точки или точки
изменения знака завихренности), то есть точки, в которых интенсивность
завихренности, образующейся вблизи поверхности тела, имеет нулевое значение. В
этих точках, вблизи которых скорость жидкости в области незавихренного течения
близка к скорости движения тела (скорости волны), возможно появление
неустойчивости вихревого движения. Вблизи этих зон создается условие для
возникновения двойных спиральных вихрей («вихревых ударных волн первого рода»).
Другим источником особых зон потока являются районы большой кривизны, угловые
точки или линии скачка положения касательных плоскостей к поверхности тела. В
этих районах происходит явление, обычно называемое отрывом пограничного слоя,
связанное с тем, что зона присоединённой к телу завихрённости утолщается и
начинает формироваться двойной спиральный вихрь. Приближенное математическое
описание возникновения подобного рода структур было дано М.А. Басиным и Н. Ю.
Завадовским в работе [40], в которой удалось установить аналогию между
формированием двойного спирального вихря на границе потенциального течения
жидкости и ударной волной, что явилось причиной названия такого рода структур -
“вихревые ударные волны первого рода”. Благодаря диффузии завихрённости
спиральные вихри превращаются в концентрированные вихревые структуры - вихревые
пузыри. Образование вихревых пузырей характеризует возникновение специфической,
не исследовавшейся ранее подробно формы потери энергии в вязкой жидкости,
связанной с взаимодействием конвекции и
диффузии завихренности внутри вихревого пузыря.
В случае несимметричного обтекания крыла
образование вихревой ударной волны первого рода (вихревого пузыря) вблизи
острой задней кромки на засасывающей
поверхности крыла приводит, благодаря нелинейному взаимодействию с основным
потоком, к появлению новых слоев раздела («вихревых ударных волн второго
рода»). Они возникают благодаря перезамыканию (слипанию) существовавших до
этого раздельно вихревых пограничных слоев, сходящих с нагнетающей и
засасывающей поверхностей крыла.
В
результате слипания происходит отделение вихревого пузыря от движущегося тела и
формирование новой вихревой структуры, названной нами выше «вихревой
нейтральной грибовидной структурой». Она состоит из присоединенной замкнутой
вихревой волны, движущейся вместе с крылом, отделившегося от неё разгонного
вихря (вихревой ударной волны первого рода) и соединяющей их тонкой двухслойной
вихревой пелены (вихревой ударной волны второго рода) в двумерном случае. При
обтекании крыла конечного размаха вихревая пелена окаймляется постоянно
формирующимися концевыми концентрированными вихревыми пузырями (вихревыми
ударными волнами первого рода).
В результате этого процесса в системе
координат, связанной с крылом, вблизи него реализуется почти установившееся
течение с циркуляцией, определяемой из условия Жуковского – Чаплыгина - Кутта
на задней кромке [147-150].
Плавность обтекания острой задней кромки
крыла поддерживается за счёт особого типа гидродинамической устойчивости,
аналогичного интенсивно изучаемому в настоящее время режиму самоорганизованной
критичности. Любое нарушение этого условия приводит к возникновению «ударного»
обтекания задней кромки и появлению вблизи неё вихревых ударных волн первого
рода, отделение которых от поверхности крыла, изменяя циркуляцию, вновь делает
течение вблизи острой задней кромки плавным. Этот процесс позволяет практически
без затрат энергии и безинерционно обеспечивать за счёт управления углом атаки
крыла или его формой изменять поперечные силы, действующих на крыло, и
использовать крыльевые устройства в качестве несущих конструкций и управляющих
элементов самолётов, космических аппаратов, экранопланов, дельтапланов, парашютов
и судов различных типов, а также при создании лопастных механизмов: движителей,
вентиляторов, насосов, турбин, ветровых электростанций. Природа также широко
использует крылья в создаваемых ею «конструкциях». Птицы, рыбы, некоторые
млекопитающие, насекомые используют крылья в качестве несущих и управляющих
элементов и движителей. Кроме того, любой объект, несимметрично движущийся в
газообразной и жидкой среде, становится крылом, и все вышеприведённые
утверждения могут быть применены и к нему.
Изложенная выше схема формирования
условия плавного обтекания угловой задней кромки крыла использована М. А.
Басиным и И. Г. Шапошниковым для
разработки нелинейной модели обтекания крыла в рамках невязкой жидкости, обобщающей
гипотезу Жуковского- Чаплыгина- Кутта на случай произвольного нестационарного
движения крыла [143]. Эта модель в какой-то мере является аналогом модели
бифуркации рождения цикла в теории автоколебаний конечномерных динамических
систем [75].
Ранее из подобных волновых представлений
о формировании циркуляции на поверхности крыла исходил один из основоположников
теории крыла – Ф. Ланчестер [144-146]. Однако, в дальнейшем, благодаря успехам,
достигнутым в локальном анализе характеристик крыльев, основанном на постулате
Жуковского – Чаплыгина - Кутта [146-150],
волновому характеру обтекания крыла внимания уделялось мало.
Значительно усложняется картина течения
при движении крыла в неоднородной сплошной среде, в частности, вблизи свободной
поверхности жидкости, которая является новым, дополнительным источником
волновых движений. Обычно гравитационные волны малы, и для их анализа
достаточно применения результатов линейной теории. Однако, при увеличении
амплитуды и энергии гравитационных волн в районе их гребней интенсифицируется
вихревое движение, и локальная скорость в этой зоне становится близкой к
скорости перемещения волны. Предельной теоретически возможной стационарной
гравитационной волной на глубокой воде является волна Стокса с 
(
-
высота волны, 
- её
длина), в вершине которой, как и при обтекании движущегося твердого тела,
образуется критическая точка, скорость жидкости в которой равна скорости волны.
Дальнейшее увеличение энергии гравитационной поверхностной волны приводит к
появлению в её вершине сверхкритических скоростей, формированию вихревых
ударных волн, присоединенных к основной волне - к частичному или полному
разрушению волн [49-55] .(разрушение поверхностной волны вследствие
неустойчивости наступает несколько раньше).
Разрушение нелинейных гравитационных
поверхностных волн, начиная с некоторых величин переносимой ими энергии,
становится во многом эквивалентным развитию вихревых ударных волн при
несимметричном циркуляционном обтекании тела. Здесь также устанавливается
своеобразный «режим самоорганизованной критичности», прекрасно описанный поэтом
[210] и вдохновивший многих художников. Таким образом, вихревое обтекание тела
с формированием на его поверхности циркуляционного течения и поток, создаваемый
гравитационными волнами, возникающими на поверхности жидкости, могут рассматриваться
с единых позиций как нелинейные волны, связанные с деформацией или перемещением
границ раздела сред.
При движении несущего тела вблизи
границы раздела сред или в произвольной среде, в которой могут возникать
волновые движения, при определённом соотношении между геометрическими
характеристиками движущегося тела, скоростью его движения и дисперсионными
свойствами сплошной среды может возникнуть третья форма вихре - волнового и
структурного резонанса - вихре-волновой резонанс по скорости и размерам тела, присоединённой
вихревой структуры и волновой картины, интенсивность проявления которого
значительно превышает интенсивность двух первых форм вихре - волнового и
структурного резонанса. Именно эта форма резонансных явлений приводит к
аномально высокой интенсивности взаимодействия движущегося объекта с окружающей
средой.
Четвёртой формой вихре - волнового и
структурного резонанса является взаимодействие несущих тел между собой или со
структурами, формируемыми при их движении. Примерами структурно-вихревого резонансного
взаимодействия такого типа являются движение крыла вблизи экрана и переходный
режим кавитации. В последнем случае взаимодействующими волновыми структурами
являются несущее крыло и возникающая вблизи него присоединённая паровая или
газовая каверна.
Глава V. Вихре-волновой и структурный
резонанс. Концепция работает.
1. Основные параметры
движущегося тела как уединённой волны
В соответствии с концепцией вихре -
волнового и структурного резонанса, предложенной
для качественного объяснения аномальных явлений, обнаруженных при движении тел
в неоднородной сплошной среде, твёрдое или деформируемое тело, движущееся в
сплошной среде, отождествляется с эквивалентной уединённой волной (телом –
волной) [31]. При этом скорость волны,
эквивалентной телу, 
принимается равной
скорости движущегося тела 
:
,
(5.1)
а длина эквивалентной волны 
определяется по приближённой формуле:
,
(5.2)
где 
- размер тела в направлении движения.
Коэффициент 
зависит от формы
обтекаемого тела и может определяться, в случае отсутствия полного
теоретического решения конкретной задачи взаимодействия, эмпирически.
Теоретические расчеты обтекания симметричных и несимметричных тел и крыльев
дают основания предварительно определить наиболее вероятный диапазон изменения
этого параметра 
, хотя в некоторых
случаях его значение может лежать и вне этого диапазона. Основанием для принятой гипотезы могут служить
рассуждения, приведённые Дж. Лайтхиллом при анализе волновой картины около
препятствия на дне потока весомой жидкости [34]. Другим теоретическим
основанием может служить анализ результатов замены симметрично обтекаемого
тонкого тела системой источников с суммарной интенсивностью, равной нулю. Если
считать, что эти источники расположены на линии, совпадающей с направлением
движения тела, и имеют в первом приближении линейно изменяющуюся интенсивность,
то разложение распределения источников в интеграл Фурье вдоль направления
движения даст некоторую функцию от волновых чисел, максимум которой окажется в
зоне длин волн, близких к длине обтекаемого тела. А именно эта гармоника
формирует присоединенную волну в случае соответствующего выбора скорости
относительного движения.
Волновое число эквивалентной волны
определяется по формуле:
, (5.3)
а частота эквивалентной волны –
. (5.4)
2.
Классификация вихре - волновых и структурных резонансов.
Качественный
анализ теоретических и экспериментальных данных и разработка новых
математических моделей позволили создать классификацию резонансных процессов
между движущимся телом и окружающей средой,
включающую:
1. резонансное возбуждение движущимся (и (или)
колеблющимся) телом или системой особенностей определённой волновой картины,
включающей лишь один набор волн из возможного спектра волн в окружающей
сплошной среде - резонанс по скорости и частоте;
2. структурно-волновой резонанс по скорости и размерам, когда
размеры тела соизмеримы с размерами присоединённой волновой системы;
3. вихре - волновой резонанс по скорости, размерам тела и
параметрам вихревых структур, формируемых около движущегося несимметричного
тела в среде, в которой возможно появление диспергирующих волн, границ раздела
и вихревых структур, возникновение которого определяется дополнительным
условием плавного обтекания кормовой части тела (постулатом Жуковского -
Чаплыгина – Кутта), приводящий к резкому изменению циркуляции потока около
тела, а следовательно, сил взаимодействия между телом и сплошной средой.
4. резонансное взаимодействие через среду нескольких
несимметричных тел, движущихся в
сплошной среде, или тел с границами раздела сред и (или) вихревыми структурами
(структурный резонанс) .
Два первых
типа явлений были известны ранее и исследовались при решении различных
прикладных задач. Однако не был достаточно чётко прояснён их резонансный
характер. Третий и четвёртый типы вихре - волнового и структурного резонанса
либо не изучались вовсе, либо не рассматривались ранее как резонансные явления.
Указанные
типы резонансов могут возникать при движении тел в средах, в которых формируются диспергирующие волны, автоволны,
границы раздела сред и фаз, а также
вихревые и грибовидные структуры различной природы или при обтекании
препятствий , а также ниш и отверстий. К этому типу резонансов можно отнести
также процесс взаимодействие квантовой частицы с потенциальной ямой или
барьером, что позволяет применить концепцию вихре-волнового и структурного
резонанса к исследованию процессов, происходящих в микромире и изучению явления
самоорганизации при анализе нано-процессов. Однако для всех возможных
разнообразных форм этого резонансного явления могут быть определены общие
необходимые условия его возникновения и существования, знание которых позволяет
предсказывать, находить и изучать и воссоздавать различные формы этого
необычного феномена.
3.
Дисперсионные свойства сплошной среды.
Рассмотрим общий случай движения тела в сплошной
среде (поле), внутренняя динамика которого описывается некоторым линейным или
нелинейным оператором, воздействующим на полевые потенциалы. В среде, в которой
движется тело, обычно справедливо дифференциальное уравнение в частных
производных для основной функции распределения скалярного, векторного или
тензорного параметра, определяющего
характеристики потока.
,
(5.5)
где 
- некоторый линейный или нелинейный оператор. Этому оператору
обычно соответствует определённый собственный спектр линейных и нелинейных волн
или структур, между элементами которых существует система спектральных
соотношений
, (5.6)
где 
и 
частоты и волновые
числа элементарных волн, которые могут быть возбуждены в сплошной среде.
Решая
последнее уравнение относительно , получаем
. (5.7)
Скорость перемещения элементарной волны
определяется её длиной
.
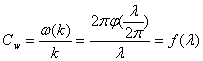(5.8)
4.
Резонанс по скорости.
При равномерном поступательном движении тела картина волн, формирующихся вблизи
тела, перемещается вместе с телом, оставаясь неизменной. Это широко известное
явление имеет резонансную природу, так как движущееся тело формирует около себя
устойчивую волновую картину только из тех волн, проекция скорости которых
совпадает со скоростью движения тела. Оно было названо нами резонансом по
скорости.
На основании условия резонанса по
скорости может быть определена структура волн, присоединённых к телу, или в
частном случае, одной резонансной присоединенной волны, что и было сделано рядом
авторов для случая корабельных волн [34], [118].
Волны других
длин имеют скорости, меньшие или большие, скорости движения тела, и в случае
двумерного обтекания уходят от тела вперёд и назад, не формируя устойчивой
резонансной картины. При установившемся движении с телом движется лишь одна резонансная волна или лишь
одна волновая картина .
В
соответствии с предлагаемой концепцией основным необходимым условием структурно
волнового резонанса по скорости является условие равенства скоростей тела и
присоединённой волновой картины, что приводит к равенству:
(5.9)
или
. (5.10)
Таким образом, в стационарном потоке за
препятствием или впереди него формируется волновая картина, определяемая
скоростным резонансом, в простейшем случае представляющая синусоидальную волну,
волновое число которой определяется скоростью движения тела или скоростью
набегающего на препятствие потока и спектральными характеристиками среды. В
случае сложных форм зависимости волнового
числа от скорости потока, когда функция 
многозначна
или бесконечнозначна, резонансная картина волн, присоединённых к движущемуся
телу, может стать достаточно сложной, например, трёхмерная волновая картина при
движении судна, описанная выше [34,110, 111, 118].
5.
Околозвуковое и сверхзвуковое движение тел.
Характерным является пример
присоединённых ударных волн при трансзвуковом и сверхзвуковом движении тел в
жидкости или газе. Дисперсия волн в этом случае практически отсутствует. Поэтому
при скоростях, меньших скорости звука, резонансный режим по скорости не
наступает. Присоединённых к движущемуся телу волн нет. Если скорость движения
тела равна скорости звука, то функция становится в линейном приближении бесконечнозначной и
наступает скоростной резонанс практически со всеми волнами звукового спектра.
Потенциальная возможность резонансного роста амплитуд волн различной длины
порождает присоединённую к движущемуся телу нелинейную ударную волну.
В
действительности, при скоростях, близких к скорости звука, за счёт нелинейных
эффектов, наблюдается дисперсия, что
усложняет волновую картину около тела, но основная закономерность
сохраняется. При скоростях движения тел,
больших скорости звука, скоростной резонанс обусловливает существование угла
Маха при формировании присоединённых волн [211-214 ].
6.
Движение тела на мелководье
В некотором смысле противоположная
картина наблюдается при движении судна на предельном мелководье. В этом случае
в жидкости существует предельная скорость диспергирующих волн, определяемая
соотношением:
, (5.11)
где 
- ускорение силы тяжести, 
- глубина водоёма или толщина слоя воды. При приближении
скорости судна, а следовательно, скорости присоединённой волны к 
дисперсионное соотношение для поверхностных волн вырождается,
и волны всех длин приобретают скорость, близкую к предельной. Скоростной
резонанс в этом предельном случае проявляется в формировании в носовой части
движущегося судна мощной поперечной волны [215]. В случае, если скорость
движения судна несколько превышает
предельную скорость волны, волновая картина практически полностью
исчезает. Этот эффект был открыт в Англии в XIX веке. Вот что пишут по этому поводу Дж. Лайтхилл и
цитируемый им Скотт-Рассел [34]:
«Некоторые интересные следствия вытекают
из того факта, что скорость волн на воде глубины 
не может превышать 
. Это означает, что если скорость потока 
, то не существует решения (уравнения для дисперсионного соотношения), описывающего волны с
перпендикулярными направлению распространения гребнями. Препятствия общей формы
ещё могут создавать волны с наклонными к направлению движения гребнями… С
другой стороны, препятствие, близкое по форме к перекрывающему поток цилиндру и
создающее значительные волны с гребнями под прямым углом к потоку, когда 
, не может породить такие волны, когда , и обычно создаёт слабые наклонные волны.
Аналогично, широкая баржа, почти
перекрывающая канал, по которому она движется, испытывает внезапное понижение
сопротивления, когда её скорость превышает . Главный член в волнообразующем сопротивлении … исчезает, и
сохраняется только намного меньший член, обусловленный возникновением наклонных
волн по бокам баржи.
Скотт Рассел писал в
Этот же
эффект был использован проф. А. М.
Басиным при решении ряда задач об оптимизации форм судов, движущихся на
мелководье [215-220], а также А. М. Басиным И. О. Веледницким, А. Г. Ляховицким
и Е. И. Степанюком, предложившими принципиально новые типы судов, движущихся со
сверхкритическим скоростями в условиях ограниченного фарватера [221-228 ].
Подробный теоретический анализ изменения
нелинейной волновой картины при переходе
через критическую скорость движения на
мелководье выполнен Д. В. Маклаковым [156]. Он показал, когда и при каких условиях
нелинейность приводит к формированию за обтекаемым препятствием различных типов
волновых движений: волн Стокса, кноидальных волн, солитонов.
Аналогичных резонансных явлений следует
ожидать при обтекании потоком малой глубины местных заглублений на дне потока,
над которыми также возникает
присоединённая волновая картина.
7.
Структурно- волновой резонанс по скорости и продольному размеру.
Другой волновой параметр, который может
определять резонансное взаимодействие, это длина волны. Если длина волны,
эквивалентной движущемуся телу, становится близкой к размерам присоединённой к
движущемуся телу волновой картины, то амплитуды волновых и вихревых возмущений
сплошной среды достигают максимального значения. Необходимым условием этой
второй формы структурно- волнового резонанса является равенство в направлении
движения тела длин волн, эквивалентных телу, и длин волн, захваченных
движущимся телом или формируемыми им вихревыми или дипольными структурами.
.
(5.12)
Используя соотношения
(5.13)
и условие скоростного резонанса
,
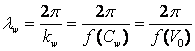(5.14)
получаем
необходимое условие структурно- волнового резонанса по скорости и
размерам:
; (5.15)
или
. (5.16)
Отсюда определяется зависимость скорости
движения тела, соответствующей режиму структурно-волнового резонанса, от длины
тела в направлении его движения и дисперсионных характеристик среды.
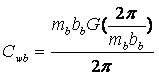(5.17)
Здесь 
- скорость, при которой длина присоединённой к движущемуся
телу волны равна длине волны, эквивалентной движущемуся телу.
Количество значений
резонансной скорости при резонансах второго типа для данной длины тела
определяется числом значений функции 
при заданном значении
длины волны.
8.Основной
безразмерный параметр вихре - волнового и структурного резонанса.
Проведённые
рассуждения позволяют ввести в рассмотрение безразмерный параметр вихре -
волнового и структурного резонанса по скорости и размерам:
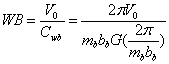. (5.18)
В случае, если в среде движутся два тела или тело
взаимодействует с вихревыми структурами, возникающими в сплошной среде и
движущимися вместе с ним, например, с паровой или воздушной каверной при
движении тела в жидкости, величина 
определяется по более
простой формуле
. (5.19)
Здесь:
- длина вихревой структуры или каверны в направлении движения
тела;
- поправочный коэффициент, который может быть, так же, как и
для тела, принят лежащим в диапазоне 
.
Если форма движущегося тела и сопутствующей ему
вихревой структуры близки или исследуется резонансное взаимодействие двух
близких по форме тел, то величина резонансного параметра определяется по
простой формуле
.
(5.20)
Необходимым условием существования вихре
- волнового и структурного резонанса второго и более высоких классов является
равенство скорости движущегося тела 
и - скорости, при
которой длина присоединённой к движущемуся телу волны равна длине волны,
эквивалентной движущемуся телу. Резонанс может наступить, когда безразмерный
параметр вихре - волнового и структурного резонанса станет равным единице
. (5.21)
Пусть
в некоторой сплошной среде имеются две взаимодействующие с ней структуры и
пусть в течение некоторого промежутка времени они оказались на незначительном
расстоянии друг от друга. Тогда, если их размеры близки, то мы вправе ожидать
при их взаимодействии через среду (поле) проявления аномальных явлений,
связанных с вихре - волновым и структурным резонансом. Тем самым, область
поиска возможных проявлений этого явления существенно расширяется.
9.
Горб волнового сопротивления тел в ограниченном фарватере как результат
резонансного взаимодействия второго класса.
Концепция
вихре - волнового и структурного резонанса и эффективность введения
специального резонансного числа подтверждается теорией и практикой
проектирования судов и кораблей, движущихся
как в глубокой жидкости, так и в условиях мелководья. В этом случае
дисперсионное соотношение для гравитационных волн в жидкости может быть
записано в виде:
. (5.22)
Подставляя это соотношение в формулу (5.18), получаем:
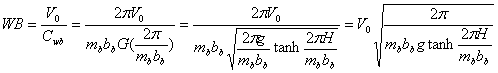. (5.23)
Введём, как это принято при
исследовании движения тел в весомой жидкости, безразмерное число Фруда по длине
тела:
(5.24)
и безразмерную относительную глубину жидкости
.
(5.25)
Тогда параметр структурно - волнового резонанса
запишется в виде
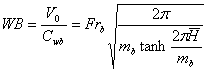. (5.26)
В рассматриваемом случае резонансный параметр зависит
от трёх безразмерных величин: числа Фруда по длине тела в направлении движения 
, поправочного коэффициента для эквивалентной волны 
и относительной глубины
водоёма (или потока) . Если относительная глубина потока стремится к
бесконечности, то 
. Соотношение (5.26) перестаёт зависеть от относительной
глубины бассейна и существенно
упрощается:
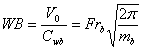. (5.27)
В случае малой относительной глубины фарватера имеем :
. (5.28)
Формула для также существенно
упростится и примет вид:
. (5.29)
Резонансный параметр перестаёт зависеть от длины
движущегося тела.
В общем случае, воспользовавшись
условием резонанса по скорости и размерам , получим следующее соотношение:
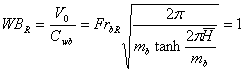(5.30)
Отсюда резонансное число Фруда по длине движущегося
тела определяется формулой:
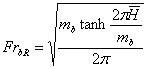. (5.31)
С уменьшением относительной глубины
бассейна среднее значение резонансного числа Фруда по длине тела уменьшается,
одновременно сужается и диапазон резонансных значений этой величины. Однако,
растёт величина другого безразмерного
резонансного параметра, числа Фруда по глубине водоёма, 
, формула для определения которого принимает вид:
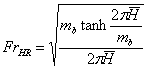. (5.32)
При 
, значение резонансного числа Фруда по длине тела определяется
формулой 
и стремится к нулю.
При этом резонансное значение числа Фруда по глубине водоёма
стремится к своему
критическому значению 
, не зависящему от длины тела. Все длины волн становятся
резонансными по скорости и резонансный эффект должен существенно усиливаться. В
некоторых случаях целесообразно ввести новый параметр - число Фруда по глубине
бассейна и длине тела.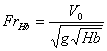 
, зависимость резонансного значения которого от параметров
относительного движения определяется соотношением
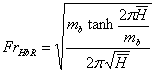(5.33)
Хотя при предельных значениях глубин водоёма
резонансные значения этого параметра стремятся к нулю, однако в широком
диапазоне отношений глубины к длине тела его значения меняются мало .
Эти выводы
качественно подтверждаются результатами расчётов волнового сопротивления речных
судов, выполненных А. Г. Ляховицким под руководством А. М. Басина [215] а также
экспериментальными данными. Положение горба волнового сопротивления судов, для
которых проводились расчёты и выполнялись модельные эксперименты для глубокой
воды лежит в предсказанном исходя из концепции структурно-волнового резонанса
диапазоне чисел Фруда по длине судна. С уменьшением глубины водоёма зона
резонансных значений, соответствующих горбу волнового сопротивления сужается,
тогда как сам горб, являющийся результатом резонансного взаимодействия всё
большего числа компонент Фурье разложения формы тела с диспегирующими волнами
сплошной среды, растёт по интенсивности. В пределе, когда резонансные значения
числа Фруда по глубине стремятся к критическому значению, горб коэффициента
волнового сопротивления оказывается максимальным, и характер зависимости его
положения от скорости не зависит от длины судна.
Существование
резонансных скоростей движения судов оказывает существенное влияние на
оптимальную форму и конструктивные особенности судов, предназначенных для
различных скоростных режимов [229]-[232].
10.Резонансные
явления при движении тел в стратифицированной жидкости.
Приведём
ещё один пример использования резонансного параметра, который может служить
основанием для развития нового направления исследований резонансного
взаимодействия движущихся тел с неоднородностями сплошной среды. При
горизонтальном движении тел в непрерывно стратифицированной сжимаемой жидкости
или газе (океане или в атмосфере) в плоскости 
, где ось
совпадает с
направлением движения тела, а ось 
направлена вертикально
вверх, приближённое дисперсионное соотношение для продольных волн, направление
движения которых совпадает с направлением движения тела, имеет следующий
вид:[31, 34]
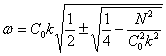, (5.34)
где
;
(5.35)
- равновесное распределение плотности по высоте, являющееся
непрерывно убывающей функцией высоты,
-скорость звука невозмущённого течения при давлении 
и распределении
плотностей - равна отношению приращения давления к приращению плотности
при постоянной энтропии.
При больших значениях имеют место две
значительно отличающиеся друг от друга частоты волн
.
(5.36)
.
(5.37)
В первом случае (5.36) скорость звуковой волны не
зависит от её длины и резонанс по длине совпадает с резонансом по скорости, что
резко сужает зону резонансных скоростей и расширяет зону резонансных длин волн. Этот случай был кратко описан нами ранее
при анализе резонанса по скорости для трансзвуковых течений около тел.
Второй случай (5.37) характеризует
независимость волновой частоты от волнового числа, тогда как скорость волны
обратно пропорциональна волновому числу и прямо пропорциональна её длине.
Подставляя
общее выражение для дисперсионного соотношения (5.34) в формулу для
резонансного числа, получим
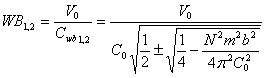(5.38)
или после преобразований
.
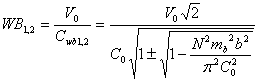(5.39)
Рассмотрим отдельно значения 
.
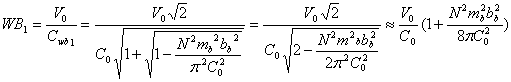. (5.40)
Необходимое условие наступления вихре - волнового и
структурного резонанса примет вид
. (5.41)
Если ввести, как это обычно принято в аэродинамике,
число Маха
(5.42)
то резонансное
число Маха, определится по приближённой формуле
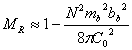(5.43)
Формула (5.43) показывает, что значительные градиенты
плотности в атмосфере могут привести к возникновению вихре - волнового и
структурного резонанса и сопутствующих ему неблагоприятных воздействий на
динамику летательных аппаратов не только при трансзвуковых, но и при
околозвуковых скоростях движения. Это явление, если оно возникнет, может
явиться причиной аварии летательного аппарата и поэтому потенциальная
возможность его появления требует специального дополнительного изучения.
Второй
вариант резонансного числа в первом приближении может быть представлен в виде
. (5.44)
Исходя из необходимого условия
возникновения вихре - волнового резонанса
,
(5.45)
определяем величину резонансной скорости движения
тела.
(5.46)
Из условия
(5.46) следует важный вывод: скорость движения тела, соответствующая
резонансному обтеканию, уменьшается до
нуля при 
.
Этот
предсказанный теоретически результат может иметь такое же принципиальное
значение, как и само явление вихре – волнового и структурного резонанса. В
соответствии с ним, с уменьшением степени неоднородности жидкости резонансная
скорость перемещения тела стремится к нулю. Следовательно, вихре – волновой и
структурный резонанс по скорости и размерам теоретически возможен даже при
очень малых неоднородностях сплошной среды и малых скоростях движения тела. Это
физическое явление может быть использовано для индикации слабых неоднородностей
в сплошной среде и на его основе могут быть сконструированы приборы,
обеспечивающие такую индикацию.
Так как входящая в определение резонансного числа
величина 
является функцией от ускорения
свободного падения 
, то природные гравитационные
аномалии также могут повлиять
на условия возникновения вихре-волнового
и структурного резонанса.
11. Вихре
- волновой резонанс при движении крыла вблизи границы раздела сред . Численный
и качественный анализ. Сопоставление теории с экспериментальными данными
. У несимметрично обтекаемых тел –
крыльев имеется одна существенная особенность, отличающая их от симметрично
обтекаемых тел. Благодаря условию плавного обтекания задней кромки таких тел
(постулат Жуковского-Чаплыгина-Кутта) вокруг контура их продольного сечения
формируется присоединённая вихревая структура с зависящей от геометрии тела и
условий обтекания суммарной циркуляцией. Эта присоединённая к движущемуся телу
вихревая структура, имеющая размеры, близкие к размерам тела, и являющаяся
головной частью нейтральной грибовидной структуры [30-34 ], в свою очередь
способна резонансно взаимодействовать как с самим телом, так и с
диспергирующими волнами окружающей среды. При движении несимметричных тел в
среде может возникнуть тройной резонанс, приводящий к аномальным изменениям не
только волновой картины около движущегося тела, но и циркуляции вокруг несущих
систем, а следовательно, к резкому изменению сил, действующих на тело.
Критериями, определяющими возможность
появления такого резонанса, как и в случае резонанса второго типа, являются
во-первых, равенство единице числа вихре - волнового и структурного резонанса
и, во-вторых, асимметрия движущегося тела по отношению к направлению скорости его движения или асимметрия
обтекания тела.
Подробное
описание аномальных резонансных явлений
при движении крыла вблизи свободной поверхности воды, открытых группой
исследователей под руководством одного из авторов, явившихся одним из оснований
для введения в рассмотрение концепции вихре-волнового и структурного резонанса
приведено выше, а также дано в монографии [31] .
Попытаемся
рассмотреть эти результаты с позиций концепции вихре-волнового и структурного
резонанса. При движении крыла вблизи границы весомой жидкости имеются два типа
вихре - волновых структур: вихревой пограничный слой на поверхности крыла и
вихревой след за ним, а также диспергирующие поверхностные волны.
Основным
безразмерным управляющим параметром, определяющим условия возникновения вихре -
волнового резонанса в случае движения крыла вблизи свободной поверхности
весомой жидкости неограниченной глубины является число Фруда 
, где 
- скорость движения, 
- длина тела в направлении движения, 
ускорение силы
тяжести. Условием появления вихре - волнового и структурного резонанса при
установившемся движении крыла, так же как и ранее, будем считать равенство
скоростей тела и присоединенной гравитационной волны 
и
соизмеримость размеров присоединенной волны в районе тела с его длиной (длина
тела должна составлять определенную часть присоединенной волны. Приравнивая скорости движения и длины волн
движущегося тела и свободной гравитационной волны в жидкости, получаем
приближенное условие возникновения нелинейного вихре - волнового резонанса
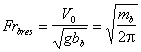. (5.47)
Если предположить, что величина 
должна изменяться в пределах от 1.0 до 2.0, то
получаем: 
.
Именно в этом диапазоне чисел Фруда, как
показали результаты представленных выше расчётов, наблюдаются основные
резонансные явления при движении крыла в диапазоне относительных глубин 
. Сдвиг в критических значениях числа Фруда, соответствующих
максимуму влияния на относительной толщины профиля, объясняется
различным характером резонансного взаимодействия.
При меньших значениях относительных
глубин 
характер волнового
движения вблизи крыла несколько изменяется. Крыло, являясь источником
возмущения, одновременно начинает играть роль локального дна, расположенного на
малой глубине под свободной поверхностью воды. В этом случае характер
поверхностных волн, их поведение вблизи крыла становятся все ближе к поведению
волн на предельном мелководье, скорость которых в пределе соответствует
величине 
,
где 
- глубина воды, в данном случае - глубина погружения крыла.
Именно поэтому с уменьшением глубины погружения происходит уменьшение
резонансного значения числа Фруда по хорде крыла и увеличение со стремлением к
единице резонансного значения числа Фруда по глубине. По той же причине в
промежуточном диапазоне относительных
погружений крыла более предпочтительно в качестве наиболее стабильного
параметра, определяющего вихре- волновой резонанс использовать число Фруда по
хорде крыла и глубине его погружения.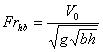 
, резонансное значение которого слабо зависит от
относительного заглубления крыла 
.(смотри рис.4.2).
12. Качественный анализ
нелинейных эффектов.
Концепция нелинейных вихревых ударных
волн, разработанная при классификации волн, вихрей, структур и систем, кроме предсказания
режимов движения, в которых следует ожидать резонансного взаимодействия тела с
внешней средой, позволяет оценить также, в каких случаях и по каким причинам
линейная теория может давать результаты, отличные от экспериментальных данных.
На её основе можно также предсказать типы структур, которые сформируются в результате резонансного
взаимодействия.
Так, например, при анализе результатов
расчётов гидродинамических характеристик подводного крыла по линейной теории
было получено, что при резонансном значении числа Фруда над задней кромкой
крыла должен круто подниматься склон кормовой волны, высота которой по расчетам
может быть значительно выше предельной (см. рис 5). Как следует из концепции
вихревых ударных волн и теоретических оценок, такая волна неустойчива и на
вершине её должна формироваться вихревая ударная волна первого рода -
концентрированный вихрь (или каскад пространственных концентрированных вихрей в
виде брызг), диаметр которого при относительных глубинах, меньших 
,
соизмерим с глубиной погружения крыла. Этот вихрь должен поглощать часть
свободной границы, которая под действием сил тяжести и поверхностного натяжения
теряет устойчивость, что приводит к тому, что при устойчивости в целом
глобального вихревого и волнового движения течение внутри формируемой в
кормовой части вихревой ударной волны становится хаотическим, однако волна
продолжает оставаться над кромкой крыла, двигаясь вместе с ним. Между тем,
как следует из качественного анализа
формирования вихревых ударных волн на крыле, подъёмная сила может значительно
измениться только тогда, когда сформировавшийся вблизи задней кромки концевой
вихрь (вихревая ударная волна первого рода), сходит с поверхности крыла
(формирование вихревой ударной волны второго рода).
В резонансном режиме существует взаимное
усиление роста циркуляции и роста кормовой волны за крылом. Разрушение кормовой
волны на поверхности воды должно приводить к тому, что концентрированные вихри,
образующиеся вблизи задней кромки крыла, не смогут отделяться от кромки, и рост
циркуляции, а также энергии волны, формирующейся за крылом, прекратится. Таким
образом, нелинейность при вихре - волновом резонансе должна приводить к тому,
что очень большие величины
, полученные на основании линейной теории при малых
относительных заглублениях не должны реализовываться. При этом
результатом нелинейного взаимодействия может оказаться новая вихревая
структура, формирующаяся вблизи задней кромки крыла, включающая в себя как
элементы вихревую ударную волну, формирующуюся на свободной поверхности воды в
результате разрушения волны, и концевой вихрь, возникающий вблизи задней кромки
крыла.
13. Результаты экспериментального исследования
проявлений вихре - волнового и структурного резонанса.
Результаты
экспериментальных исследований, в которых был изучен вихре-волновой резонанс при обтекании
подводного крыла, сводятся к следующему.
Теоретически
было предсказано, что при относительных скоростях движения крыла, лежащих в
диапазоне чисел Фруда для 
и при 
)
должны возникать интенсивные резонансные явления. Анализ этих явлений ,
выполненный с позиций квазилинейной теории и концепции вихревых ударных волн
показал , что при резонансных значениях чисел Фруда вблизи крыла возможно
появление разрушающихся волн и формирование новых вихре - волновых структур. В
опытовых бассейнах были проведены испытания крыльевого устройства прямоугольной
формы в плане с удлинением 
(
-
размах крыла) с плоско - выпуклым сегментным профилем продольного сечения
(относительная толщина 
) в
широком диапазоне относительных глубин погружения и чисел Фруда. Испытания
проводились при углах атаки 
.
Особое внимание уделялось измерению гидродинамических характеристик и
визуализации картины течения в критическом диапазоне чисел Фруда и
относительных глубин погружения. Как и было предсказано теоретически, получены
значительные отрицательные значения подъемной силы крыла даже при положительных
геометрических углах атаки. При 
и 
наблюдаются значения 
Как это и предсказано на основании концепции
вихревых ударных волн, экспериментальные данные для 
по сравнению с резонансными значениями,
полученными по линейной теории, наоборот, сильно разошлись: они оказались
значительно меньше расчётных. Кроме
того, анализ выполненных фотографий подтвердил теоретические выводы о
формировании в указанном диапазоне чисел Фруда и относительных глубин
погружения при всех исследованных углах атаки над задней кромкой крыла разрушающейся
волны. При малых углах атаки экспериментально обнаружена носовая разрушающаяся
волна иной формы, имеющая плоскую вершину, покрытую нестационарными “бурунами“.
Носовая волна уменьшается с увеличением угла атаки, и при 
практически исчезает: тенденция к исчезновению
носовой волны с увеличением угла атаки подтверждается результатами расчетов по
линейной теории . Вне указанного резонансного диапазона чисел Фруда при 
, как и предсказано расчетами , происходит качественное
изменение картины течения. Вершина кормовой волны смещается назад и практически
сразу исчезает носовая волна. С удалением от крыла присоединенной кормовой волны резко увеличивается значение 
.
Величина коэффициента подъёмной силы проходит через нуль и с дальнейшим
увеличением скорости принимает положительные значения (если 
).
Течение вблизи крыла становится плавным с малыми волновыми деформациями на
поверхности жидкости . При этом измеренные величины подъёмной силы крыла
практически совпадают с данными, полученными по линейной теории. Предсказания о
расхождении значений между результатами линейной теории и
экспериментом, основанные на концепции вихревых ударных волн первого и второго
рода, качественно подтвердились . Эксперимент показал также существование новой
. не изучавшейся ранее формы разрушения нелинейной носовой волны. Диапазон
чисел Фруда и относительных погружений, соответствующий возникновению
аномальных гидродинамических явлений в эксперименте практически полностью
совпал с теоретически предсказанным диапазоном, что еще раз подтвердило
основные положения на которых строился теоретический анализ.
14.Вихре-волновой резонанс в стратифицированной
сплошной среде. Теоретические предсказания.
Другим характерным примером
вихре-волнового резонанса является несимметричное движение тела вблизи границы
раздела сред различной плотности. Если неподвижная среда (жидкость или газ)
имеет внутреннюю границу раздела, и плотность нижней жидкости 
., а верхней - 
., то дисперсионное соотношение для внутренних волн
записывается в виде:
или
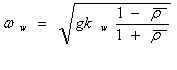, (5.48)
где 
. Частоты и скорости волн, соответствующих одним и тем же
волновым числам, оказываются тем меньше, чем больше отношение и в случае, когда
отношение плотностей стремится к единице, частоты и скорости перемещения
внутренних волн стремятся к нулю. Воспользовавшись необходимым условием возникновения
вихре – волнового и структурного резонанса и введя обобщённое
денситометрическое число Фруда:
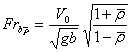, (5.49)
легко показать, что при 
условию возникновения вихре-волнового
и структурного резонанса должно соответствовать соотношение:
(5.50)
или
.
(5.51)
Если 
, то число Фруда 
, при котором возникает резонанс, также стремится к нулю.
Этот теоретический результат, хотя ему может быть найдено разумное объяснение,
и он соответствует ранее полученному соотношению для непрерывно
стратифицированной жидкости или газа, является удивительным и имеет
фундаментальное значение. Малые скачки плотности и малые изменения скорости
движения тела могут привести, вследствие вихре - волнового и структурного
резонанса, к значительным возмущениям и появлению новых вихре - волновых
структур в стратифицированной среде.
Теоретические расчеты и
экспериментальные данные по определению волнового сопротивления тел, движущихся
вблизи границ раздела, подтверждают эту гипотезу (явление «мёртвой воды») [34].
Так как зона параметров движения, при которой возникает вихре - волновой
резонанс в стратифицированной среде, очень узка, явление резонанса явно
проявляется в природных явлениях редко. Однако, возмущения, связанные с
возникновением этого явления, столь велики, что могут стать причиной аномальных
природных явлений и аварий подводных аппаратов и самолётов.
Одним из
авторов совместно с Ю. В. Кафтанниковым теоретически исследована третья форма вихре - волнового и структурного
резонанса при движении крыла в стратифицированной весомой сплошной среде [31].
Как следует из результатов расчётов (рис. ), резонансные значения коэффициентов
подъёмной силы слабо меняются с уменьшением скачка плотности сплошной среды,
тогда как скорость, при которой возникает вихре - волновой резонанс, стремится
к нулю. Малые скорости движения в слабо - стратифицированной среде вызывают
существенные резонансные возмущения коэффициентов нормальных к направлению
движения сил, действующих на движущиеся тела.
Полученный
теоретический результат имеет такое же принципиальное значение, как и само
явление вихре - волнового и структурного резонанса, и требует
экспериментального подтверждения.
В случае
получения соответствующих экспериментальных данных обнаруженный эффект может
найти широкое применение при измерении с помощью использования эффектов,
связанных с вихре - волновым и структурным резонансом, малых неоднородностей в
сплошной среде, в том числе и вредных примесей, плотность которых отличается от
плотности основной части среды. На принципе вихре - волнового и структурного
резонанса может быть построен новый класс приборов, являющихся индикаторами
слабых неоднородностей плотности и полевых потенциалов в сплошных средах
Кроме того, результаты расчетов
показывают, что уменьшение неоднородности слабо изменяет воздействие крыла на амплитудные
характеристики гравитационных волн, возникающих в среде, то есть относительная
интенсивность резонансного воздействия падает незначительно. Нелинейные
эффекты, связанные с формированием новых вихревых структур, должны сохраняться
вплоть до чрезвычайно малых неоднородностей и чисел Фруда.
Однм из
авторов совместно с Н.В. Корневым был разработан вихревой метод решения трехмерных уравнений
Навье - Стокса, использование которого, по-видимому, позволит прояснить в
будущем расчетным методом детали вихре - волновых резонансных явлений
[162]-[168] .
В последние
годы большое внимание уделяется изучению волновых явлений в атмосфере и океане,
где неоднородность по плотности и скорости течений вызывает широкий спектр
диспергирующих волн, движущихся в различных направлениях. Кроме того, в
неоднородной сплошной среде вследствие гидродинамической неустойчивости
формируются нелинейные волны, а также вихревые и грибовидные структуры [82].
Взаимодействие этих волн и структур с движущимися телами должно вызвать широкий
спектр вихре - волновых резонансных явлений рассмотренных выше типов, условия
возникновения которых определяются на основании построения в каждом конкретном
случае частной модификации резонансного параметра .
15.
Движение крыла вблизи экрана как проявление четвёртой формы вихре – волнового
резонанса. Биологические и технические приложения.
Вихре - волновой и структурный резонанс
может возникнуть и при взаимодействии несущих тел между собой и с границами
среды. Наиболее известным примером аномального изменения гидродинаических
характеристик несущего тела является движение крыла вблизи экрана. Как показано
в большом количестве теоретических и экспериментальных исследований, обобщённых
в ряде статей, монографий и в справочных материалах (смотри например [121])
движение несущего тела (крыла) вблизи твёрдой границы сопровождается аномальным
ростом подъёмной силы крыла и резким падением индуктивного сопротивления. Этот
эффект похож по своим проявлениям на явление структурного резонанса. И может
быть объяснён с позиций разрабатываемой
концепции.
Резонансный характер этого режима может
быть объяснён следующим образом. Влияние экрана на подъёмную силу крыла
теоретически может быть заменено эквивалентным влиянием симметрично расположенного
относительно экрана крылом.
При таком рассмотрении указанного течения
мы находим объекты вихре – волнового и структурного резонанса – это два крыла,
движущиеся с одной скоростью и имеющие одинаковые хорды, расположенные
симметрично друг относительно друга. Если эти крылья рассматривать как две
уединённые вихревые волны, то существуют все необходимые условия для вихре –
волнового и структурного резонанса.
В случае двух крыльев, поступательно
движущихся с одинаковыми скоростями на незначительном расстоянии друг от друга
условие возможности появления вихре - волнового и структурного резонанса
соответствует формуле (5.20)
, (5.52)
где 
- хорда 
того крыла. Теоретические расчёты показывают, что резонансное
взаимодействие, приводящее к росту аэродинамического качества, максимально,
когда крылья расположены симметрично друг другу относительно плоскости,
параллельной направлению их движения и расстояние между крыльями стремится к
нулю. Именно этот резонансный случай и эквивалентен с аэродинамической точки
зрения движению крыла вблизи экрана. Следует обратить внимание ещё на одну
особенность указанного резонансного режима. Подъёмная сила крыла при приближении
к экрану растёт обратно пропорционально расстоянию до экрана или, что
аналогично, расстоянию между крыльями. А подъёмная сила приближённо
пропорциональна циркуляции крыла. Таким образом, два движущихся симметрично
друг относительно друга крыла за счёт вихре - волнового и структурного
резонанса формируют дипольную структуру, интенсивность которой при малых
расстояниях между крыльями не зависит от величины этого расстояния. Отсюда
можно сделать вывод о том, что хотя бы в некоторых случаях формирование дипольных
(грибовидных) структур может явиться результатом вихре - волнового и
структурного резонанса. Что подтверждает сделанный нами ранее на основе
простейшей математической модели вывод о резонансном характере формирования
грибовидных структур.
К широкому спектру приложений влияния
экранного эффекта на несущую способность крыльев следует добавить ещё одно
направление использования этого типа резонанса, а именно применение эффекта
резонансного взаимодействия несущих систем к созданию принципиально нового компьютерного
метода распознавания образов, который позволит осуществить распознавание
одновременно как по глобальным, так и по локальным масштабам.
Кроме того, возникает идея о том, что в самом
общем случае процесс распознавания образов, то есть отбора среди многих
возможных таких, которые соответствуют данному, может быть построен на принципе
структурно- волнового или вихре - волнового и структурного резонанса.
.Более сложные резонансные явления
должны происходить при обтекании несущих систем в жидкости малой глубины.
Наряду с резонансными взаимодействиями с волнами на свободной поверхности
крыло резонансно взаимодействует с дном.
«Экранный резонанс» может значительно
усилиться вихре-волновым резонансом крыла с гравитационными волнами при
установке несущих конструкций в потоке малой глубины. Такие конструкции могут
служить мощными волнопродукторами либо волногасителями, а также основными
элементами волновых электростанций
Возникающий здесь резонанс, четвёртого
порядка может привести к гигантской концентрации энергии и его использование
позволит построить новые конструкции,
например, возбуждающие и гасящие энергию волн, в том числе и волн
цунами.
16. Качественный анализ кавитации подводных крыльев в
режиме вихре - волнового и структурного резонанса.
Ещё
более необычный эффект, который также может быть отнесён к структурно -
вихревому резонансу четвёртого типа, был подробно исследован нами при
кавитационном обтекании подводных крыльев и лопастей гребных винтов быстроходных
судов
Многочисленные теоретические и экспериментальные
исследования показали, что именно в этом
режиме кавитационного обтекания крыльев наблюдаются аномальные явления,
связанные со значительным ростом подъёмной силы крыла и толщины каверны, приводящие
к потере устойчивости и интенсивным колебаниям каверны с формированием
вихревого следа, обладающего универсальными частотными характеристиками, не
зависящими от формы профиля и угла атаки крыла.
Для того,
чтобы применить к рассматриваемому случаю качественный анализ, основанный на
теории вихревых ударных волн, и концепции вихре-волнового и структурного
резонанса, рассмотрим с волновой точки зрения паровую или воздушную каверну,
присоединенную к движущемуся телу. Формирующаяся около тела присоединённая
каверна, заполненная газом или паром, с деформируемой границей раздела
плотности и фаз с позиций разработанной классификации нелинейных волновых
движений, вихревых и грибовидных структур и транспортно-информационных систем,
так же, как и твердое тело, может рассматриваться в качестве поступательно
движущейся уединённой волны, скорость которой равна скорости тела (тем самым
первое условие вихре - волнового и структурного резонанса для присоединенных
каверн уже выполнено), а длина которой однозначно связана с длиной каверны :
.
При этом с
достаточной степенью достоверности (вследствие аналогичной геометрии) можно
считать, что коэффициент 
для движущегося в
жидкости тела и 
для формирующейся
около него каверны равны между собой .
Поэтому в данном случае необходимое условие
возникновения вихре- волнового и структурного
резонанса, имеющее в общем случае вид,
значительно упрощается и принимает форму
,
что полностью соответствует условию резкого роста
амплитуд обеих введенных нами в рассмотрение нелинейных волн, полученному при
решении квазилинейной задачи. Источники определяют толщину каверны, т.е.
амплитуду нелинейной волны, ей соответствующей, а циркуляция, в соответствии с
концепцией вихревых ударных волн первого и второго рода, определяют амплитуду
присоединенной к телу циркуляционной волны, являющейся головной частью
формирующейся при движении крыла грибовидной структуры.
Концепция
вихревых ударных волн позволяет, как и в случае движения крыла в неоднородной
сплошной среде, не только предсказать условия возникновения вихре - волнового и
структурного резонанса, но и построить схематизированную картину нелинейного
вихре - волнового и структурного взаимодействия, указать на отличие реальной
картины течения от предсказанных по квазистационарной теории и качественно
проанализировать новые структуры, которые получаются в результате резонансного
взаимодействия.
Резонанс
должен приводить не только к увеличению амплитуд обеих взаимодействующих волн:
каверны и циркуляционной волны около крыла,-
но и к совместной глобальной потере ими устойчивости, (аналогичной
бифуркации рождения цикла в обычных динамических системах) в результате которой
формируются периодически возникающие грибовидные структуры, создающие за
кавитирующим крылом кармановскую дорожку, основные параметры которой
определяются размерным резонансным параметром - хордой крыла. Возникают
автоколебания каверны и нелинейные автоволны в виде сложной системы, головную
часть которой представляют резонансно взаимодействующие крыло и каверна,
движущиеся со скоростью движения тела, а хвостовую- кармановская дорожка
связанных грибовидных структур, формирующихся из пограничного слоя на
поверхности крыла и свободной границы каверны).
Если
проанализировать качественно картину развитой кавитации за телом (двумерное
течение), то можно выделить три основных типа нелинейных волновых структур:
расположенное впереди движущееся поступательно со скоростью 
твердое тело, присоединенную к нему
деформируемую, заполненную газом или паром каверну и след, который можно
схематизировать кармановской дорожкой связанных грибовидных структур.
Границы
каверны, которые могут считаться также поверхностями скачка завихренности,
принципиально не могут формировать установившегося течения, так как в этом
случае в хвостовой части должна была бы существовать седловая точка, а жидкость
вливалась бы внутрь полости, пока не заполнила бы её .
В действительности, тенденция к возвратному течению
жидкости внутрь каверны в хвостовой её части существует. Благодаря ей внутри
каверны формируются области завихренности в паровой (газовой ) фазе. Сама
граница каверны окаймляет область, занятую завихрённой сплошной средой. Однако,
стационарная картина течения неустойчива, и периодически происходит
формирование вихревых структур, в результате чего в следе за телом периодически
формируются связанные свободные грибовидные структуры - кармановская дорожка
свободных вихрей.
Собственная
скорость перемещения структур кармановской дорожки отлична от скорости
перемещения тела и каверны. Кроме указанных выше трех типов вихре - волновых
структур существует переходная зона, в которой происходит периодическое
формирование грибовидных структур кармановской дорожки.
При
увеличении длины каверны, благодаря большему влиянию пространственности течения
и поперечной неустойчивости крупные вихревые структуры становятся менее
интенсивными. Переходная зона занимает все меньшую относительную часть каверны
и, находясь вдали от тела, оказывает все меньшее влияние на колебание его
гидродинамических характеристик. Структура и основные размеры формирующейся
кармановской дорожки определяется в случае развитой кавитации поперечным
размером каверны в хвостовой её части, а
точнее говоря, связанной с этим размером амплитудой изменения длины каверны за
время формирования очередного периода кармановской дорожки. Именно этот
параметр, в соответствии с концепцией вихревых ударных волн, определяет
временные и пространственные масштабы формирующихся грибовидных структур,
топологическая картина которых одинакова как при обтекании плохообтекаемых тел,
так и при обтекании тел с развитыми кавернами. Именно этим объясняется близкое
к постоянному значение числа Струхала формирования кармановской дорожки,
построенного по характерному размеру тела или каверны, которые её формируют.
В случае
развитой кавитации угол атаки обтекаемого тела лишь изменяет относительную
толщину каверны и увеличивает частоту формирования кармановской дорожки. При
малых углах атаки толщина каверны при постоянной длине практически линейно
зависит от угла атаки, а следовательно линейно от этого параметра зависит и
период формирования кармановской дорожки .
Несколько
иную картину можно представить при качественном анализе с позиции концепции
вихревых ударных волн частичной кавитации на тонком профиле крыла, поставленном
под малым углом атаки .
При больших
значениях числа кавитации и малых углах атаки в кормовой части профиля сечения
крыла формируется вихревая ударная волна второго рода с разгонным вихрем,
вихревой пеленой и образующейся на крыле циркуляцией, величина которой
определяется с помощью введения гипотезы Чаплыгина- Жуковского.
Вблизи
носовой кромки профиля также образуется присоединенная вихревая ударная волна
первого рода - концентрированный вихревой пузырь, размеры которого обычно
невелики по сравнению с размерами крыла. Существуют такие углы атаки и числа
Рейнольдса, когда вихревой пузырь, благодаря влиянию вязкой диффузии и
структуры потенциального внешнего потока оказывается практически стационарным.
Именно такая модель теоретического расчета
ламинарных и турбулентных пузырей заложена в расчетных схемах, используемых в
настоящее время различными авторами. .
В зоне
существования малых вихревых пузырей, расположенных обычно вблизи передней
кромки крыла, и формируются частичные присоединенные каверны. Эта гипотеза
положена Э.Л. Амроминым и А.Н. Ивановым
в основу предложенной ими теоретической модели формирования
присоединенных каверн при исследовании масштабного эффекта возникновения
кавитации, которая в настоящее время интенсивно развивается Э. Л. Амроминым.
Кавитационный пузырь, так же, как и формирующий его вихревой пузырь,
первоначально является стационарным, и его возникновение практически не сказывается
на суммарных гидродинамических характеристиках крыла. Уменьшение числа
кавитации приводит к росту размеров каверны. Наконец, наступает такой момент,
когда сил поверхностного натяжения и вязкостных сил уже недостаточно для
преодоления тенденции к возникновению неустойчивости в хвостовой части каверны.
В этом районе начинает формироваться возвратное течение, которое образует
периодически отделяющиеся от основной каверны полые вихревые пузыри - каверны и
образующиеся в пограничном слое вихревые пузыри противоположного знака,
интенсивность которых благодаря влиянию трения оказывается ниже, чем
интенсивность сходящих сверху полых вихревых пузырей. Это несоответствие
циркуляций полых и пристенных вихревых структур компенсируется изменением
циркуляции крыла в целом, что, в свою очередь, приводит к периодическому
формированию концевых вихрей вблизи задней кромки крыла. Таким образом, с крыла
в режиме частичной кавитации также сходит кармановская дорожка вихревых
(грибовидных) структур, причем верхний
ряд представляет собой след от колеблющейся каверны, а нижний - ряд вихрей,
сходящих с задней кромки крыла. Основное отличие этой кармановской дорожки от
той, которая возникает из развитой каверны, заключается в том, что нижние
вихревые структуры сходят одновременно не с теми вихревыми структурами, которые
вызвали их появление, а сдвинуты по отношению к ним в пространстве. Между
верхними и нижними вихрями до схода с крыла отсутствует непосредственное
взаимодействие. Кармановская дорожка как бы расщеплена в пространстве и во
времени (её верхние и нижние структуры не взаимодействуют между собой).
Как
показывают теоретические расчеты, начиная с относительной длины каверны 
, возникает резонансное взаимодействие
параметров каверны с циркуляционным течением вокруг крыла, которое теоретически
проявляется в неограниченном росте относительной толщины каверны и циркуляции
крыла . Исходя из концепции вихревых ударных волн, можно также предсказать, что
одновременно с ростом амплитуды стационарных волн: толщины волны - каверны и
циркуляционной волны около движущегося тела ,- должен наблюдаться нелинейный
вихре - волновой резонанс между вихревыми ударными волнами, формируемыми
каверной и крылом, на котором возникает периодически изменяющаяся подъемная
сила. При этом, если при малых длинах каверны возникала несинхронизированная
кармановская дорожка вихрей, параметры которой зависят от ширины каверны , то в
резонансном случае должна формироваться единая резонансная кармановская
дорожка, основные размеры которой при 
определяются
хордой крыла .
Колебания
каверныв этом режиме должны быть максимальными и равными длине каверны.
Теоретические исследования кавитирующих
крыльев с длиной каверны, равной хорде крыла, позволили определить связь
параметров резонансного режима кавитационного обтекания с формой профилей
крыльев, предназначенных для бескавитационного и околозвукового обтекания, а
также профилей, обладающих максимальным коэффициентом подъёмной силы. Построена
универсальная диаграмма, охватывающая широкий класс профилей такого типа [121].
Подробные
экспериментальные исследования переходного режима кавитационного обтекания
крыла выполнялись, начиная с середины 60-х годов. В ходе проведенной серии
экспериментов на гидродинамических стендах и в кавитационных трубах измерялись
мгновенные параметры течения около кавитирующего крыла. Исследовались
зависимости от времени следующих относительных параметров течения: мгновенной
длины присоединённой каверны 
, её
ширины 
,
протяженности зоны , в которой формируется вихревая ударная волна первого рода
(длины обратной струйки ) , параметры структуры концентрированных вихревых
объемов за движущимся крылом, являющихся результатом формирования вихревых
ударных волн второго рода, образующихся в результате самопересечения границ
каверны и вихревого насадка вблизи задней кромки крыла. Картина обтекания
фиксировалась с помощью скоростной киносъёмки (1000 - 2000 кадров в секунду).
Одновременно с визуализацией структуры течения измерялись мгновенные и средние
значения подъемной силы и сопротивления крыла. Эксперименты проводились с
крыльями различных профилей (
,
где 
-
максимальная толщина профиля , 
- хорда
крыла) в диапазоне чисел кавитации 
,
(где 
давление в потоке перед крылом, 
давление
в каверне.) 
и углов атаки 
. При этом главное внимание уделялось
исследованию присоединенных каверн, начинающихся в районе носовой кромки крыла .
Анализ полученных кинограмм позволил четко
выделить резонансный “переходный режим кавитационного обтекания крыла» . Как
показали результаты киносъемки, подтверждаются предсказания качественной модели
, полученной на основании концепции вихревых ударных волн. Действительно,
переходный режим обладает специфическими, свойственными только ему и
универсальными для него параметрами, определяемыми нелинейным резонансным
взаимодействием циркуляционного обтекания крыла с образованием вихревых ударных
волн вблизи задней кромки и течения с формированием вихревых ударных волн на
границах присоединенной каверны. Частота колебаний размеров каверны и суммарных
сил, действующих на крыло, когда максимальная длина каверны близка к хорде
крыла, а следовательно, близки и их волновые частоты, определяется тем условием
, что число Струхала 
, где 
-частота
колебаний . При этом амплитуда колебаний каверны приблизительно равна её длине
и определяется резонансным параметром - хордой крыла . Основные параметры вихре
- волновых структур в этом режиме кавитационного обтекания практически не
зависят ни от формы профиля крыла , ни от его угла атаки, ни от числа
кавитации.
Результаты экспериментов подтвердили предсказания,
основанные на концепции вихревых ударных волн, о том , что картина течения в
резонансном переходном режиме является результатом нелинейного резонансного
взаимодействия кавитационного и циркуляционного обтекания крыла, которое
приводит не только к взаимному увеличению толщины каверны и циркуляции на крыле
, но и к синхронизации следа: формированию единой резонансной вихревой дорожки
периодически образующихся вихревых ударных волн второго рода, верхний ряд
которой является результатом формирования вихрей, отделившихся от границы
каверны, а нижний ряд - следствием образования аналогичных вихревых сгустков в
зоне вблизи задней кромки крыла. Соединяющая их вихревая пелена формируется как
комплексная двойная граница раздела , частицы одной части которой ранее
принадлежали границе каверны . а другой - пограничному слою на крыле.
17. О возможности обнаружения
новых форм вихре-волнового и структурного резонанса.
Вихре - волновой и
структурный резонанс может проявиться и иметь свои специфические формы при
любых относительных перемещениях произвольных тел и неоднородной сплошной
среды, что дает возможность применять основные теоретические положения,
позволяющие изучать это и другие нелинейные явления к судостроению и авиации,
техническим производствам, химии, биологии, океанологии и метеорологии, физике
и магнитной гидродинамике
Предсказанное теоретически и
обнаруженное экспериментально явление
вихре- волнового и структурного резонанса вносит коренные изменения в
существующие представления о взаимодействии различных объектов и окружающей их
среды. Знание его природы и основных критериев возникновения позволяет
теоретически предсказать, экспериментально обнаружить и объяснить не
исследованные ранее аномальные режимы при движении тел в жидкости, газе и
других сплошных средах.
Обнаруженное явление вихре - волнового и
структурного резонанса может найти аналогии не только в гидродинамике тел,
движущихся в неоднородной жидкости и газе, но и во всех тех случаях,. когда
какая-либо жесткая или деформируемая система перемещается в неоднородной среде
или происходит взаимодействие вихревых и грибовидных структур с окружающими их
объектами или полем. Разработанная теория и выдвинутая концепция позволяют
предсказывать условия, при которых следует искать аналогичные явления.
Особого
внимания заслуживает тот обнаруженный при изучении обтекания несущих тел
теоретический результат, что при уменьшении степени неоднородности среды
резонансные явления, почти не затухая, перемещаются в зону очень малых
скоростей относительного движения тела и сплошной среды. Это позволяет
использовать открытое явление как эффективный индикатор малых неоднородностей в
среде и устройство управления, так как в этом случае при резонансе значительный
эффект может быть достигнут без существенных затрат энергии.
Значение полученных результатов состоит
не только в обнаружении и изучении нового неизвестного ранее класса резонансных
процессов и вихре - волновых структур, но также и в том , что разработанная
концепция и классификация волновых и вихревых движений позволяет предсказывать
и обнаруживать неизвестные ранее формы вихре - волнового взаимодействия,
создавать искусственно условия для возникновения этих явлений и разрабатывать
способы их предотвращения применительно
к практическим задачам, а также создавать новые способы и разрабатывать новые
конструкции, которые могут найти
применение также в различных областях техники и научных исследований. Широкое
поле деятельности открывается также для изучения физических явлений и вихре -
волновых структур, которые могут сформироваться при взаимодействии резонансного
потока с другими типами волновых и колебательных движений.
Так как при исследовании биологических и
социальных явлений наблюдается широкий спектр колебательных процессов и
волновых структур, то концепция вихре-волнового и структурного резонанса может
оказаться полезной при исследовании этих процессов, происходящих в различных
масштабах, от клетки – до биосферы [65]. Автоволны, ревербераторы,
диссипативные структуры, повсеместно возникающие в биологических объектах и во
многих химических процессах, могут резонансно взаимодействовать с движущимися
относительно них деформируемыми структурами, что должно привести к новым, не
известным ранее, или известным, но не объяснённым, особенностям аномального поведения. Именно в
биологии, экологии и социальных науках могут быть найдены новые формы
проявлений вихре- волнового и структурного резонанса. Предложенная концепция
может явиться основой для объяснения не решённых ещё проблем, связанных с
необходимостью объяснения размеров и
скоростей перемещения биологических объектов [75].
Заключение
Обобщённая концепция вихре - волнового и
структурного резонанса.
Анализ полученных теоретических и
экспериментальных результатов показывает, что нелинейное вихре - волновое
резонансное взаимодействие циркуляционного вихревого течения около движущихся в
неоднородной сплошной среде тел с волновыми движениями этой среды может
приводить к появлению новых структур, представляющих собой взаимодействующие
между собой нелинейные вихревые ударные волны и грибовидные структуры.
Критерием для предсказания указанных аномальных явлений должны являться
совпадение или кратность длин, скоростей или частот нелинейных периодических
или одиночных волн, образующихся и взаимодействующих между собой.
Концепция вихре - волнового и
структурного резонанса может иметь далеко идущие теоретические обобщения,
применение которых к различным частным случаям позволит предсказать и объяснить
многие необычные явления, возникающие при взаимодействии структур и систем
различной природы.
Приведённые выше примеры резонансного
взаимодействия свидетельствуют о возможности существовании вихре - волновых и
структурных резонансов при взаимодействии произвольных близко расположенных
структур, находящихся в некотором общем поле, через которое они могут
воздействовать друг на друга. Если структуры длительное время находятся вблизи
друг друга, независимо от их перемещения относительно поля, то первое
необходимое условие структурно-волнового резонанса – приближённое равенство
скоростей нелинейных волновых структур, выполняется автоматически.
Вторым необходимым условием структурного
резонанса является равенство эквивалентных длин волновых структур. Это условие
выполняется, когда соответствующие размеры взаимодействующих через поле
структур близки.
Для проверки возможности существования и форм проявления
структурно-волнового резонанса достаточно знать основные параметры поля, в
котором расположены взаимодействующие структуры, основное уравнение,
описывающее динамику поля, найти собственный спектр линейных и нелинейных волн,
характеризующих это поле. Для большинства известных полей, особенно полей,
описываемых линейными операторами, эта задача в той или иной степени решена
(частные случаи таких решений рассмотрены нами выше). Для простейшего
одномерного случая, когда поле удовлетворяет линейному уравнению в частных
производных, эта задача решается в общем случае. Для более сложных случаев в математике
и физике разработана теория линейных и нелинейных операторов [206].
Воздействие структур на поле обычно
описывается некоторыми интегральными операторами, характеризующими изменение
поля под действием движущихся и излучающих структур. При этом не все параметры
структур, воздействующие на поле, должны быть закреплены. В этом случае
обратное действие поля на ту же самую или другую структуру может резонансно
увеличивать (или уменьшать) не закреплённые параметры структуры. Условия
резонанса остаются теми же. Совпадение длин и частот обобщённых волн и
геометрическая близость структур между собой в течение некоторого промежутка
времени.
В
каждом частном случае может быть построено приближённое математическое описание
взаимодействия и определены условия возникновения вихре - волнового и
структурного резонанса при взаимодействии структуры и поля, а также при
взаимодействии нескольких структур через поле.
Как следует из выполненного
теоретического анализа и экспериментального изучения некоторых проявлений вихре
- волнового и структурного резонанса, резонансное взаимодействие приводит к
отбору и усилению тех волновых частот и длин волн и структур, которые являются
близкими для резонансно взаимодействующих объектов. Отсюда следует, что может
оказаться справедливым не только утверждение о том, что вихре - волновой и
структурный резонанс может быть использован для распознавания образов или
обнаружения слабых неоднородностей в сплошных средах и полях различной природы,
но также утверждение о том , что если такой отбор и такое усиление в каких-либо
явлениях наблюдается, то сам этот факт может в ряде случаев служить сигналом,
проявляющим вихре - волновой и структурный резонанс. При этом целесообразно
искать не только резонансно - взаимодействующие объекты, но и их резонансные
параметры. Такой подход позволит строить качественные теоретические модели
вновь обнаруженных аномальных явлений.
Остановимся теперь на том, как может
проявляться вихре - волновой и структурный резонанс в сложных транспортно -
информационных системах, часто представляющих собой иерархию волновых процессов
с различными частотами и структур с различными масштабами, взаимодействующими
между собой. Это внутреннее взаимодействие также осуществляется чаще всего
резонансным образом, за счёт связей соседних уровней иерархии и комбинационных резонансов, позволяющих
перейти от заданных частот возмущения и масштабов (волновых чисел) к частотам и
масштабам, определяемым соотношениями.
.
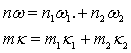Возникновение вихре- волнового и
структурного резонанса на одном уровне иерархии может резонансно же
передаваться на нижележащие и вышележащие уровни системы. Вызванные резонансным
воздействием возмущения могут нарастать и переводить систему в новое состояние
(фазовый переход) или разрушить систему.
При этом взаимодействие отдельно взятой
подсистемы с другими подсистемами может носить двоякий характер. Это может быть
ближнее взаимодействие, и тогда может проявиться и играть существенную роль
четвёртая форма вихре-волнового и структурного резонанса. Это может быть также
дальнее взаимодействие, и тогда резонансное
взаимодействие может осуществляться по схеме первой, второй и третьей
форм вихре - волнового и структурного резонанса.
В обоих случаях резонансное
взаимодействие может привести к появлению аномальных явлений и качественному
изменению поведения как отдельных элементов или подсистем или бифуркационному изменению системы в
целом.
Вихре - волновой и
структурный резонанс может проявиться и иметь свои специфические формы при
любых перемещениях произвольных структур в неоднородной сплошной среде, что
дает возможность применять основные теоретические положения, позволяющие
изучать это и другие нелинейные явления к судостроению и авиации, техническим
производствам, химии, биологии, океанологии и метеорологии, физике и магнитной
гидродинамике, экономике и других социальных процессах.
Предсказанное теоретически и обнаруженное
экспериментально явление вихре-
волнового и структурного резонанса вносит коренные изменения в существующие
представления о поведении течений около тел, движущихся в неоднородной сплошной
среде. Знание его природы и основных критериев возникновения позволяет
теоретически предсказать, экспериментально обнаружить и объяснить не
исследованные ранее аномальные режимы при движении тел в жидкости, газе и
других сплошных средах.
Открытие этого явления стимулирует
создание и развитие новых методов теоретических и экспериментальных
исследований вихревых движений в различных областях науки и техники.
Концепция вихревых ударных волн первого и
второго рода, а также осуществлённое в связи с изучением открытого явления
отождествление поля скоростей около движущегося тела и присоединенных следов и
каверн со специфическими уединенными нелинейными волнами используется для классификации нелинейных волновых
движений и объяснения известных, но не изученных до конца нелинейных явлений ,
связанных с движением тел в жидкости: отрывное обтекание тел [179],
возникновение и развитие циркуляционного течения около тела [143],
возникновение и развитие разрушающихся ударных волн на свободной поверхности
[154], обтекание интерцепторов
[180], исследование прорыва воздуха к
телам и крыльям [178], гидроупругие колебания кавитирующих и некавитирующих
крыльев [176].
Значение полученных результатов состоит
не только в обнаружении и изучении
нового неизвестного ранее класса резонансных процессов и вихре-волновых
структур, но также и в том, что разработанная концепция вихревых ударных волн и
классификация волновых движений и вихревых, грибовидных и древовидных структур
позволяет предсказывать и обнаруживать неизвестные ранее формы вихре -
волнового взаимодействия, создавать искусственно условия для возникновения
этого явления применительно к практическим задачам, а также создавать новые
способы и разрабатывать новые конструкции , часть из которых используется в
настоящее время в судостроении [180, 192, 193,, 207-209], которые могут найти
применение также в других областях техники и научных исследований.
Широкое поле деятельности открывается также
для изучения физических явлений и вихре -волновых структур, которые могут
сформироваться при взаимодействии резонансного потока с другими типами волновых
и колебательных движений колебания крыла, качке судна . вибрации, излучения и
т.д.
В последнее время предриняты
попытки обнаружения подобных явлений в биологии и науках о человеке.
Авторы высказали гипотезу о том, что
подобные явления должны быть широко распространены в биологических и социальных
процессах. В частности, вихре - волновой
и структурный резонансы могли играть существенную роль в возникновении
жизни. Эта гипотеза требует детальной теоретической проработки и может явиться основанием для
создания нового направления в изучении этой важнейшей научной проблемы.
Остановимся вкратце на возможности
применения этой концепции при экономических исследованиях. Роль неоднородной
среды в этом случае играет совокупность объектов и субъектов, между которыми
осуществляются производственные и экономические отношения. Так как в экономике
уже выработался параметр целого – деньги, то их объём, выраженный в некотором
эквиваленте может считаться своеобразным геометрическим размером субъектов
экономики. Количество денег, принадлежащих тому или иному субъекту или той или
иной корпорации может считаться её размером или длиной эквивалентной ей волны.
В экономике постоянно происходит оборот денежной массы. Период полного
обращения денежной массы того или иного субъекта экономики может считаться
частотой эквивалентной волны. А её скоростью можно считать отношение денежной
массы к периоду обращения.
Вся совокупность субъектов экономики
обладает неким свойством , которое можно считать эквивалентным дисперсионному
соотношению сплошной среды. Каждому субъекту экономической деятельности
успешному в данном поле соответствует определённая связь между его объёмом и
частотой оборота средств. Эта связь может быть экспериментально определена.
Если появляется какой-либо новый участник экономической структуры, то можно
предположить, что его деятельность будет успешной, если его капитал и предполагаемая частота его оборота будут
соответствовать дисперсиноому соотношению экономической среды, в которой он
собирается действовать. В противном, нерезонансном случае он будет иметь
неприятности. Однако указанное условие должно явиться необходимым, но не
достаточным условием успеха.
Концепция вихре-волнового и структурного
резонанса может быть после соответствующей проверки использована и при выборе
партнёров в экономической деятельности. Для
выполнения условий структурного резонанса необходимо, чтобы партнёры
имели близкие величины капитала и скорости его оборота. Если же взаимодействуют
компании с различными объёмами капитала, то в более крупной компании должно
быть подразделение, близкое по объёму к меньшей из компаний.
Литература
1.
Сунгуров А. Ю. Резонансные взаимодействия в природе.- Синергетика и методы
науки. Труды семинара. Под ред. М. А. Басина. СПб.: Наука. С. 431-433.
2.
Баранцев Р. Г. Целостность общения.- XIV Международная
конференция серии: «Нелинейный мир». Языки науки. Пущино. 3-7 июня 2006.
Сборник тезисов. Под редакцией Г. Ю. Ризниченко. С. 18.
3.
Басов Н. В. Риск - рефлексия и социальная самоорганизация» - XIV Медународная
конференция серии: «Нелинейный мир».
Языки науки. Пущино. 3-7 июня 2006. Сборник тезисов. Под редакцией Г. Ю.
Ризниченко. С. 19.
4.
Басина Г. И., Басин М. А. Синергетика. Основы методологии. – СПб.: Норма.
2006.-56с.
5.
Басин М. А., Шилович И. И. Синергетика и Internet. Путь к Synergonet. СПб.: Наука. 1999. 72 с.
6.
Басин М. А., Шилович И. И. Путь в Synergonet. СПб.:
Норма. 2004. 128с.
7.Журавлёва З.Е. И услышал я иной голос. М.: Прогресс –
Традиция, 1998. С.127. 193с.
8.Хакен Г.Синергетика. М.: Мир. 1980. 414с.
9. Арнольд В.И. Геометрические методы в теории
обыкновенных дифференциальных уравнений. Ижевск: Ижевская республиканская
типография. 2000.400 с.
10.
Ланда П. С. Нелинейные колебания и волны. М.: Наука. Физматгиз. 1997. 469 с.
11.
Мандельштам Л. И. Лекции по колебаниям. Собр. трудов. Том
12.
Басин А. М. Качка корабля. М.: Транспорт. 1969. 272 с.
13.
Арнольд В. И. Математические основы классической механики. М.: Наука. 1974. 432
c.
14.
Якубович В. А., Старжинский В. М. Параметрический резонанс в линейных
системах.- М.: Наука. Гл. ред. физ.-мат. литературы. 1987. 328с.
15.
Челомей В. Н. Парадоксы в механике, вызываемые вибрациями.- В. Н. Челомей.
Избранные труды. М.: Машиностроение 1989. С. 23-28. Материалы данной работы
были доложены на заседании Отделения механики и процессов управления АН СССР 7.
XII. 1982г.,
посвящённом 60-летию образования СССР, а также заседании Президиума АН СССР 27.
I. 1983г.
16.
. Андронов А. А., Витт А. А., Хайкин С.Э. Теория колебаний. Москва.
Гостехиздат.1937; Физматгиз. 1959. Наука. 1981.
17.
Рабинович М.И., Трубецков Д.И. Введение в теорию колебаний и волн. М.: Наука.
1984.
18.
Ланда П. С., Дубошинский Я. Б. Автоколебательные системы с высокочастотными
источниками энергии. – УФН. 1989. Т.158. В.4. С. 729-742.
19.
Ланда П. С. Преобразование высокочастотных электрических колебаний в
низкочастотные механические. Машиноведение 1988 №6. С. 90-95.
20.
Ланда П. С. Электромеханические преобразователи автоколебательного типа.
Вибротехника. 1991. №66.С.201-209.
21.
Шарковский А.Н. Сосуществование циклов непрерывного преобразования прямой в
себя Укр. Матем. Журнал. 1964 Т.26.№1
Сс.61-71.
22.
Feigebaum M.J. Quantitative
universality for a class of nonlinear transformations.J. Stat. Phys. 1978. V.19.№1. P. 25-52.
23. Feigebaum M. J. The onset spectrum of
turbulence Phys. Let.1979 v/74A №6 Pp375-378
24.Nauenberg M.Rudnik J. Universality and the
power spectrum at the onset of Chaos. Phys. Rev.B. 1981.V 24B№1Pp493-495
25. Kaneko K. Oscillations and doubling of
torus Progr.Theor.Phys.Japan. 1984.V.72№2
Pp. 202-215
26.Неймарк
Ю.И. , Ланда П.С. Стохастические и хаотические колебания. Москва.Наука 1987
27.
Анищенко В. С. Сложные колебания в простых системах. М.: Наука 1990.
28. Ruelle D., Takens F. On the nature of
turbulence Comm. Math.Phys. 1971.V.20№2Pp.167-192.
29. Vavriv D. M, Ryabov
V. R., Sharapov S.A., Ito H. M.Chaotic states of weakly and strongly nonlinear
oscillators with quasiperiodic excitation. Phys. Rev. E. 1996 V.53.№1Pp.103-114
30.
Милнор. Дж. Голоморфная динамика. Ижевск: НИЦ «Регулярная и хаотическая
динамика». 2000. 320с.
31.
Басин М. А. Компьютеры. Вихри. Резонансы. Волновая теория взаимодействия
структур и систем. Ч.2.СПб.: Норма. 2002. 144с.
32.
Басин М. А. внутреннее и внешнее время в динамике систем. Материалы
Международной междисциплинарной научной конференции : «Синергетика в
естественных науках» (Третьи Курдюмовские чтения). 19-22 апреля
33. Bhatnagar P. I. Nonlinear Waves in
One-dimensional Dispersive Systems. Claderon Press.Oxford. 1979. Имеется
русский перевод. Бхатнагар П. Нелинейные волны в одномерных дисперсных
системах. М.: «Мир». 1983 136 с.
34.
Лайтхилл Дж. Волны в жидкости. М.: Мир. 1981. 600 с.
35. Grawford F.S.Waves.
36. Feynman R.P., Leighton R.B. , Sands H., The
Feynman Lectures on Physics, V.3, Addison-Wesley Publishing Company , INC,
Reading,
37. Нелинейные волны. Самоорганизация.
Ред.А. В. Гапонов - Грехов, М. И. Рабинович. М.: 1983. 264c.
38.
Басин М. А., Завадовский Н.Ю. Модель двойного спирального вихря как предельная
форма свободной поверхности для нестационарного потока идеальной несжимаемой
жидкости. Труды семинара по обратным краевым задачам . Выпуск 22. Казань: КГУ. 1985.
39. Basin M. A. Wave Formation by the Motion of
Surface Ship Hydrodynamic Complex near the Free Boundary. Classification of
Nonlinear Waves. Vortex-wave Resonance. Papers of IMAM 93 Congress. Edited by
P. A. Bogdanov. Vol. II.
40.
Басин М. А. Волновой подход к исследованию структур и систем . Реальность и
субъект. Т.2. № № 2 - 3 СПб.: 1998. С. 57-72.
41.
Басин М. А. Основы классификации нелинейных волновых движений, вихрей и
транспортных систем. Синергетика и методы науки. (Под редакцией М. А. Басина)
СПб.: Наука. 1998. С. 95-131.
42.
Басин М. А. Волны. Кванты. События. Волновая теория взаимодействия структур и
систем. Ч. 1. СПб.: Норма. 2000. 168с
43.
Басин М. А. Спиральные числа. Степенные особенности. Волны. Вихри. Грибовидные
структуры. Транспортно-информационные системы.- Международная междисциплинарная
научно-практическая конференция: «Современные проблемы науки и образования».
Керчь, 27.06-4.07. 2001. Ч. 1. Харьков. 2001. С. 12-13.
44.
Басин М. А. Информационно-волновая теория структур и систем.- Материалы Второй
научной конференции Санкт-Петербургского союза учёных: «Проблемы и перспективы
междисциплинарных фундаментальных исследований. 10-12 апреля 2002 года СПб.
2002. С. 8 -9.
45.
Басина Г. И., Басин М. А. Синергетика. Эволюция и ритмы человечества. СПб.:
Норма. 2003. 260c.
46.
Басина Г. И., Басин М. А. Синергетика. Основы методологии. СПб.: Норма. 2006.
56с.
47.
Васильев В. А., Романовский Ю.М. Яхно В.Г. Автоволновые процессы.- Под ред. Д.
С. Чернавского М.: Наука Гл. ред. физ.- мат лит. 1987 – (Соврем. пробл. физики)
240 с.
48.
Режимы с обострением. Эволюция идеи. Законы коэволюции сложных структур. М.:
Наука. 1998. 255с. (Кибернетика: неограниченные возможности и возможные
ограничения).
49.
Реньи А. Трилогия о математике. М.: Мир. 1980. 376с.
50.Hadamard J. Lecons sur le propogation des
ondes.
51. Kotschin N. E. , Uber starke
Diskontinuitaten in einer kompressiblen Flussigkeit", Proceedings of the
International Congress for Applied Mechanics. Delft.1925. P.405 - 418.
52. Truesdell A. First Course in Rational
Continuum Mechanics. The
53.Russell J. S. Report on Waves. British
Association Reports. 1844.
54. Scott-Russell J. Report on Waves. Proc.
Roy. Soc. Edinb., P. 319 – 320.
55. Korteweg D. J., De Vries G. On the Change
of Form of Long Waves Advancing in a Rectangular Canal and on a New Type of
Long Stationary Waves.
56. Zabusky N. J., Kruskal M. D. Interaction of
Solitons in a Collisionless Plasma and the Recurrence of Initial States.-Phys.
Rev. Lett. V.15. 1965. P.240-243.
57.Березин
Ю. А., Карпман В. Л. О нелинейной эволюции возмущений в плазме и других
дисперсионных средах. ЖЭТФ.Т.51. 1966. С.
1557 - 1564,
58. Miura R. M., Gardner C. S., Kruscal M. D.
Korteweg – de Vries Equation and
Generalization. II. Existence of Conservation Laws and Constants of the
Motion.-J. Math. Phys. V. 9. 1966. P.1204-1209.
59. Taniuti T. , Wei C.C. Reductive
Perturbation Method in Nonlinear
60.
Кадомцев Б. Б., Карпман В.И., Нелинейные волны. УФН. 103. 1971. С.193-213..
61.Захаров
В. Е. ,Фаддеев Л. Д.,Уравнение Кортевега-де-Фриза- полностью интегрируемая
Гамильтонова система .-" Функциональный анализ" 1971 Т.5. N 4.
С.18-27.
62.Новиков
С. П. Периодическая задача для уравнения Кортевега-де- Фриза,
"Функциональный анализ "1974.Т.4. N.3. С. 54-66.
63.Newell A.C., Solitons in Mathematics and
Physics - University of
64.
Тахтаджян Л. А., Фаддеев Л. Д. Гамильтонов
подход к теории солитонов. М.: Наука. 1986. 528 С.
65.Сретенский
Л. Н. Теория волновых движений жидкости. М.: Наука. 1977 816с.
66. Stoker J.J. Water Waves
.The Mathematical Theory with Applications. Interscience Publishers ,Inc., New
York , Interscience Publishers Ltd.,
67. Маклаков Д. В. Нелинейные задачи гидродинамики потенциальных течений с неизвестными границами. М.: «Янус-К».
1997. 280с.
68.Арнольд.
В. И. Особенности каустик и волновых фронтов.М.: Фазис 1996. 334 с.
69. Tulin M.P. Supercavitating Flows. Small
Perturbation Theory, Journal of Ship Research,1964 v.7 N3.
70.Birkhoff G., Zarantonello E.H., Jets, Wakes
and Cavities ,
71.Гуревич
М.И.Теория струй идеальной жидкости. Второе издание
М.:"Наука"1979
536стр
72.
Егоров И.Т. , Садовников Ю.М, Исаев И.И., Басин М.А. Искусственная кавитация.
Л.: Судостроение 1971
73.
Варченко А.Н., Этингоф П.И. Почему граница круглой капли превращается в
инверсионный образ эллипса.М.: Наука. Физматгиз. 1995. 80с.
74.
Управление риском. Риск. Устойчивое развитие. Синергетика.
М.:
«Наука» 2000. 431с. (Серия «Кибернетика: неограниченные возможности и возможные
ограничения»).
75.
Хэссард Б., Казаринов Н., Вэн И. Теория и приложения бифуркации рождения цикла.
М.: Мир. 1985. 280 с.
76.
Басин М. А. Об одной аналогии между одномерными динамическими системами и
плоскими гидродинамическими течениями идеальной жидкости.
77. Pullin D. The Large Scale Structure of
Unsteady Self-similar Rolled up Vortex Sheets // Journal of Fluid Mechanics ,
Vol. 88, N 3 1978
78.Van Dyke M. An Album of Fluid Motion . The
Parabolic Press. Stanford, California.1982
79.
Бэтчелор Дж. Введение в динамику жидкости. М.: Мир. 1973. 760с.
80.
Басин А.М., Миниович И.Я. Теория и расчёт гребных винтов. Л.: Судпромгиз. 1963.
760с.
81.
Вилля Г. Теория вихрей.Л.-М.:ОНТИ-НКТП.1936.266с
82.
Миндлин И.М. Интегро-дифференциальные уравнения в динамике тяжёлой слоистой
жидкости. М.: Наука. Физматлит.
1996. 304с.
83. Phillips O. M. Wave Interaction . Idea
Evolution Journal of Fluid Mechanics . A Special Issue Celebrating the 25th Anniversary of the Journal and Containing
Editorial Reflections on the Development of Fluid Mechanics. Volume106, May1981
Cambridge University Press Cambridge-London-New York-New Rochelle - Melbourne
-Sydney.
84.
Басин М. А. Вихре - волновой резонанс в
гидродинамике подводного крыла. Международный симпозиум по гидродинамике судна
, посвященный 85-летию со дня рождения А.М.Басина. Л.:-1995. С. 399-407.
85.
Лорьер Ж.-Л. Системы искусственного
интеллекта. М .”Мир” 1991
86.
Кузнецов Г. И. , Москалюк С.С., Смирнов
Ю.Ф. , Шелест В.П. Графическая теория представлений ортогональных и унитарных
групп и ее физические приложения . Киев “Наукова Думка “ 1992 288 стр
87.
Клименко А. В. Основы естественного
интеллекта. Ростов на Дону . Издательство Ростовского университета. 1994. 304с
88.
Новое в синергетике .Загадки мира
неравновесных структур М.”Наука” 1996“264 с
89.
Басин М.А. Орлов С.Г. Теоретическое
исследование свободной транспортной динамической системы. Труды Семинара “
Синергетика и методы науки “ (в печати )
90.
Крылов Ю. К. Интаэрология и синергетика. - Синергетика и методы науки. (Под
ред. М. А. Басина). СПб.: Наука. 1998. С. 77-94.
91.
Крылов Ю. К. Интаэрология: принципы построения целостных систем.-
Ценологические исследования. Вып.
92.
Крылов Ю. К., Кудрин Б. И. Целочисленное аппроксимирование ранговых
распределений и идентификация техноценозов. - Цитологические исследования.
Одиннадцатый выпуск. Москва: Центр системных исследований. 1999. 80с.
93.
Басин М. А. К теории идеального трансформера. – Синергетика и методы науки.
(Ред. М. А. Басин). СПб.: Наука. 1998. С. 356-375
94.Бутусов
К.П. Золотое сечение в Солнечной системе. АН СССР Астрометрия и небесная механика.
Серия: «Проблемы исследования Вселенной.» Вып. 7, Москва-Ленинград 1978
С.475-500.
95.Сороко
Э.М. Структурная гармония систем. Минск: 1984
96.Смирнов
В.Л, Проблемы логики при моделировании самоорганизующихся структур. Синергетика
и методы науки (Под редакцией М.А. Басина) – СПб.: Наука. 1998. С. 40-63.
97.Смирнов
В.Л. Солнечный цикл: механизм формирования структуры и начальные этапы
эволюции. С.390-410
98.
Быстров М.В. О шуме 1/f c точки зрения
всеобщей гармонии. Синергетика и методы науки (Под редакцией М.А. Басина) –
СПб.: Наука. 1998. С. 375-390.
99.
Иванов- Ростовцев А.Г., Колотило Л. Г., Тарасюк Ю.Ф. Шерстянкин П.П.
Самоорганизация и саморегуляция природных систем. Модель, метод и основы теории
D-Self (Под ред. К.Я. Кондратьева. СПб.: Русское географическое
общество. 2001. 216с.
100.Буданов
В. Г. Ритмокаскады и их роль в космоземных связях.- Стратегия жизни в условиях
планетарного экологического кризиса.Т.1.СПб. 2002.С.207-218.
101.
Смирнов В.Л. Формирование комплекса узлов на основе протоструктуры. Материалы
Международной междисциплинарной научной конференции : «Синергетика в
естественных науках» (Третьи Курдюмовские чтения). 19-22 апреля
102.
Буданов В.Г. Методология синергетики в постнеклассической науке и образовании.
М.: Издательство ЛКИ. 2007. 232с.
103.
Басина Г.И. , Басин М.А. Синергетика. Основы методологии.СПб.: Норма. 2006.
104.
Маслов В.П, Квантовая экономика. М.:Наука.2005.
105
.Филиппс О.М. Взаимодействие волн - эволюция идеи. В монографии: “Современная
гидродинамика , успехи и проблемы .Редакторы Дж. Бетчелор, Г. Моффат М.: Мир.1984.С. 297-314.
106 . Michell
J. H. The Wave Resistance of a Ship. Philosophical Magazine Ser 5, 1898, Vol.
45. № 272.
107. Havelok
T.H. The Resistance of a Ship among Waves -PRSL. Ser. A 1937. Vol. 161. № 906.
108.
Кочин Н.Е. О волновом сопротивлении и подъемной силе погруженных в жидкость
тел. Труды конференции по теории волнового сопротивления. М.: Изд. ЦАГИ.
1937.С.1-30.
109. Костюков А.
А. Теория корабельных волн и волнового сопротивления. Л.: Судпромгиз. 1959.
110
. Басин А.М., Анфимов В.Н. Гидродинамика судна. Л.: “Речной транспорт”. 1961.
111 Справочник по теории корабля. В трех томах.
Под редакцией Я. И. Войткунского. Л.: «Судостроение» 1985.
112
. Келдыш М. В., Лаврентьев М. А. О движении крыла под поверхностью тяжелой
жидкости – Труды конференции по теории
волнового сопротивления
113 Седов Л. И. Плоская задача о глиссировании по
поверхности тяжелой жидкости. Труды конференции по теории волнового
сопротивления.
114 Владимиров А. Н. Подъемная сила подводного
крыла вблизи свободной поверхности. Л.: “Судостроение“. №6. 1937.
115
. Чудинов С. Н. О подъемной силе подводного крыла конечного
размаха. Труды ВНИТОСС. 1965. Т.6. Вып. 2 . Сс. 74-92.
116
Блюмин В. И., Иванов Л. А., Масеев М. Б. Транспортные
суда на подводных крыльях. М.: Транспорт. 1964.
117
Егоров И. Т.,
Соколов В.Т. Гидродинамика быстроходных судов. Л.:”Судостроение”1971, 424с.
118
Эпштейн Л. А.
Методы теории размерностей и подобия в задачах гидромеханики судов .
Л.”Судостроение”. 1970
119
Федоров Е. А.
Плоская задача о движении тела произвольной формы под свободной поверхностью
идеальной невесомой жидкости. Труды НТО СП. 1968 . Вып. 104. С. 126-133.
120
Логвинович Г. В. Гидродинамика течений со свободными
границами Киев.: “Наукова думка”. 1969. 216 с.
121
. Басин М. А. Шадрин В. П. Гидро- аэродинамика крыла вблизи границы раздела
сред . Л.: Судостроение. 1980. 304с.
122
. Панченков А.Н. Исследование движения подводного крыла вблизи свободной
поверхности жидкости. Автореферат диссертации. Киев 1962
123 . Nishiyama T. Lifting line theory of the
submerged hydrofoil of finite span”, Parts 1,2,3. Journal of the American
Society of Naval Engineers. 1959-1960. Vol. 71-72
124 . Isai
W.H. Zur Theorie der nahe der Wasseroberflache fahrenden Tragflacher . Ing Arch
27(1959/60) S.295
125
Панченков А. Н. Гидродинамика подводного крыла. Киев.:
«Наукова думка» 1965. 552 с.
126
Salvesen N.(1981) “Five Years of Numerical Naval Ship Hydrodynamics at
DINSPDC” // J. Of Ship Research. Vol.25. № 4
Pp. 219-235
127 Басин
М.А. О силах, действующих на крыло, движущееся вблизи свободной поверхности
весомой жидкости. Доклад на конференции: “ Гидродинамика крыла , движущегося
вблизи свободной поверхности жидкости , и глиссирующих поверхностей». Л.:1982.
128 Ткач
А. Я. О влиянии весомости среды на гидродинамические характеристики несущей
поверхности . Доклад на конференции: ”Гидродинамика подводного крыла .
движущегося вблизи свободной поверхности
жидкости и глиссирующих поверхностей.“ Л.:. 1982.
129
. Макасеев М. А. К решению плоской
задачи обтекания тонкого гибкого профиля под поверхностью тяжелой жидкости .
Доклад на конференции Гидродинамика подводного крыла . движущегося вблизи
свободной поверхности жидкости и
глиссирующих поверхностей.“
130
. Лотфуллин М.В. Движение
системы профилей под свободной поверхностью весомой жидкости . Доклад на
конференции: «Гидродинамика подводного крыла . движущегося вблизи свободной
поверхности жидкости и глиссирующих поверхностей.» Л.: 1982.
131 Лордкипанидзе А.Н. Расчет гидродинамических
характеристик тонкого крыла большого удлинения и сопоставление результатов
расчета с экспериментальными данными. Доклад на конференции «Гидродинамика
подводного крыла . движущегося вблизи свободной поверхности жидкости и глиссирующих поверхностей.»Л.:1982.
132
Ткач А. Я. О влиянии весомости среды на
гидродинамические характеристики несущей поверхности Проблемы гидродинамики
судна. Труды ЛКИ .Л.Изд-во ЛКИ. .1983. С.76-82.
133
Басин М. А., Лордкипанидзе А.Н., Ткач А. Я. Явление вихре-волнового резонанса при исследовании
гидродинамических характеристик подводного крыла, движущегося вблизи свободной
поверхности весомой жидкости . Труды НТО СП . Вып.
134
Басин М.А.,
Лордкипанидзе А.Н., Ткач А.Я. Решение задачи о стационарном движении несущей
поверхности вблизи границы раздела сред. Вихре-волновой резонанс. Труды НТО СП.
Вып.1. Л.:
135.
Корнейчук А. А. Квадратурные
формулы для сингулярных интегралов . Численные методв решения дифференциальных
и интегральных уравнений и квадратурные формулы. 1964 т.4 №4 Сс.64-74.
136
Мишкевич В.Г. О
построении квадратурных формул для сингулярных интегралов , встречающихся в
гидроаэродинамике . Вопросы судостроения . Серия : “ Проектирование судов “
1980. Вып. 23 С. 98-108
137
Гребные винты .
современные методы расчета ( Бавин В. Ф.,Завадовский Н.Ю., Левковский Ю.Л. ,
Мишкевич В.Г)., Л.: “ Судостроение “1983. 236 с.
138
Лотфуллин М.В. Филиппов С.И. Обтекание профиля весомой
жидкостью вблизи границ раздела сред. Механика машиностроения . Тезисы докладов
II республиканской научно-технической конференции . Секция механики жидкости,
газа и плазмы . Брежнев. 1987. С. 44.
139
Щигунов В.Г. Решение нелинейных нестационарных
волновых задач вихревым методом. Канд. диссертация . СПб.: СПбГМТУ.
140 Duncan G. G. An
Experimental Investigation of Breaking Waves Produced by a Towed Hydrofoil
//Proc.R. Soc.London.1981. Vol.A377.
141
Basin M.A. A Wave Formation by the Motion of
Surface Ship Hydrodynamic Complex near the Free Boundary. Classification of
Nonlinear Waves. Wave-vortex Resonance.// Papers of IMAM 93 Congress/ Ed. by
P.A. Bogdanov. Vol.II. Varna.
142
Басин М.А.
Основы классификации нелинейных волновых движений , вихрей и транспортных
систем //Синергетика и методы науки. Под. ред. М.А.Басина. СПб. «Наука» 1998.
Сс.95-131.
143
Басин М. А.,, Шапошников И.Г. Новая модель
нестационарного течения около крыла в невязкой жидкости. Математическое и
физическое моделирование в гидродинамике судна . Труды НТО СП . Выпуск
144
Lanchester F. W.
Stability of an Aerodrome. Доклад на собрании Бирмингемского общества. 19 июля
1884.
145. Lanchester F. W. Aerodynamics.
146.
Аэродинамика . Под общей редакцией Р.Ф. Дюренд. Том I. ОНТИ НКТП СССР . 1937.
436 с.
147..Жуковский
Н. Е О наивыгоднейшем угле наклона аэропланов. Воздухоплавание и исследование
атмосферы. Вып.1. 1897
148. Kutta W.
M. Auftriebskrafte in stromenden Flussigkeiten. Illustrierte aerodinamische
Mitteilungen. 1902. S.133.
149.
Жуковский Н.Е. О присоединенных вихрях . Сообщена автором в Московском
математическом обществе 15 ноября 1905 и напечатана в трудах отделения
физических наук ОЛЕ т. XIII. Вып.2 1906.
150.
Чаплыгин С.А. О давлении плоско-параллельного потока на преграждающие тела .
Московский математический сборник №28 . 1910.
151.
Longue -Higgins M. S., Fox M. J.H. Theory of the almost -highest Wave . The Inner
Solution . -Journal of Fluid Mechanics. 1977 V.80 . Pр.721-742.
152. Юэн Г. Лэйк Б. Нелинейная динамика гравитационных волн на глубокой воде. Механика.
Новое в зарубежной науке. №.41. М.: Мир. 1987. 184 с.
153
Нелинейные волновые процессы . Механика. Новое в зарубежной науке №.42 . М.:
Мир. 1987. 296 с.
154
Амромин Э.Л., Басин М.А. Бушковский В.А. Два решения пространственной задачи о
предельных волнах на поверхности весомой жидкости. Прикладная математика и механика т.54. N1. 1990.
155. Xu H., Yue D.K. P. Numerical Study of
Three-dimensional Overturning Water Waves// Proc/ of 7th Int.
Workshop on Water Waves and Floating Bodies. 1992. Pp.213-216.
156. Маклаков Д.В.
Нелинейные задачи гидродинамики потенциальных течений с неизвестными границами.
М.: «Янус-К». 1997. 280 с.
157.
Басин М.А. Об изменении вектора суммарной завихренности сплошной среды при движении
в ней твердого тела и при движении ее внутри твердого сосуда. ИАН СССР.
Механика жидкости и газа №1 М.: 1984.
158.
Басин М.А. Изменение моментов поля завихренности жидкости при движении в ней
твердого тела// Совершенствование ходовых , мореходных и маневренных качеств
судов. Материалы по обмену опытом. Вып.
159.
Басин М.А. Основные уравнения вихревого движения жидкости. Вихре-волновой
резонанс. Материалы по обмену опытом. Труды НТО СП. Л:.Судостроение.
1990.
161 Basin M. A. Basic Equations of Vortex Fluid
Motion. Selected Papers.Vol.1. Applied Hydrodynamics. St-Petersburg.
162. Басин М.А., Корнев Н.В., Захаров А.Б. Аппроксимация трехмерных вихревых полей. Труды Центрального
научно-исследовательского института морского флота. СПб.:1993. 184-196.
163.
Басин М.А., Корнев Н.В. Аппpоксимация поля завихpенности в неогpаниченной
сpеде. ЖТФ РАН, Ноябpь, 1994, CПб. Сс. 179-185
164. Basin M.A., Kornev N.V. New Computational
Method of Vortex Dynamics. Report on the Euromech Colloquium 315.
165. Basin M.A., Kornev N.V.Approximation of
Vorticity Field in an Unbounded Volume. Tech. Phys. 39 (11) 1994, American
Institute of Physics. Pp.1184-1187
166.
Basin M.A., Kornev N.V. Vortex Methods in Hydrodynamics. International
Symposium on Ship Hydrodynamics Devoted to 85-th Anniversary of Birthday of
167 . Basin M.A., Kornev N.V. Berucksichtigung
der Reibung in der Wirbelmethode. ZAMM.78 №5 1998.Ss.29-52.
168. Basin M.A.Kornev N.V.
169 Басин М.А., Лордкипанидзе А.Н., Ткач А.Я. Гидродинамические характеристики несущего комплекса, движущегося вблизи свободной поверхности весомой жидкости. Труды
Семинара по краевым задачам. Выпуск 26 Аэродинамика течений с неизвестными
границами Казань: КГУ 1991.Сс.29-59
170. Basin M.A.,
Lordkipanidze A. N., Tkach A. Ja. Vortex-Wave
Resonance in the Hydrodynamics of Foil, Moving near the Interface of the
Different Density Media // Waves and Vortices in the Ocean and their Laboratory
Analogues. The Fifth Annual Workshop of the Commission on the Problems of the
171.Басин
М.А. Основы классификации нелинейных волновых движений и вихревых структур.
Явление вихре-волнового резонанса при движении несимметричных тел в неоднородной
жидкости// Проблемы гидромеханики в освоении океана Материалы конференции по
прикладной гидромеханике Киев ИГМ АНУ 1992 Сс.192-193
172
Basin M.A. Wave Formation by the Motion of a Surface Ship Hydrodynamic
Complex near the Free Boundary . Classification of Nonlinear Waves. Wave-Vortex
Resonance. Proceedings of the VI Congress of the IMAM. Edited by Peter A.
Bogdanov . Volume II, 15-20 November 1993.
174.
Басин М.А. Вихре-волновой резонанс// Синергетика и методы науки. Труды
семинара. . Oтветственный редактор M.А. Басин. С.-Пб.“Наука” 1998 .c.415-418.
175. Егоров И. Т. , Садовников Ю.М. ,Исаев И. И.
Басин М. А. Искусственная кавитация , Л. “Судостроение”1971. 284 с.
176.
Басин М.А. Лабок Л.Ю. Шалларь А.В. О связи режима обтекания и гадроупругих
колебаний крыльевых систем быстроходных судов. НТО СП. Материалы по обмену
опытом. Вып. 186 Л:”Судостроение”.1972 Сс.76-87.:
177.
Егоров И.Т., Басин М.А., Садовников Ю.М., Шалларь А.В. Методика
экспериментального исследования нестационарных гидродинамических характеристик
кавитирующих подводных крыльев. НТО Судпрома. Экспериментальная гидродинамика
судна. Материалы по обмену опытом
Вып.190. Л.: ”Судостроение”, 1972. Сс94-100
178 Basin M.A., Shaposhnikov,
179. Basin M.A., Borisov R.V., Greengoltz A.I.,
Guseev A.S. Kagan I.S Theoretical and Experimental Determination of the Forces
of Viscous Nature by the Vibration of the Bodies at the Fluid. Proceedings
of XV Ubileum Seminar on the Ship
Hydrodynamics.
180. Басин М. А., Бочагов В. И., Мизина М. Я.,
Охрименко Г. Г., Пономарев А. В., Сидоров В.П. , Титов В. Г. Результаты
теоретико -экспериментальных исследований несущих поверхностей с интерцeпторами . Доклад на Всесоюзном семинаре по отрывным
течениям. Новосибирск 1988.
181. Князева Е.Н.
Курдюмов С.П. Законы эволюции и самоорганизации сложных сиситем. М.: Наука.
1994. 238 с.
182. Синергетика и методы науки (Ред. Басин М.А.)
СПб.: Наука 1998. 440 с.
183. Баранцев Р.Г. Синергетика в современном
естествознании. М.: 2003.
184. Данилов Ю. А. Причудливый ми науки.
Саратов.Изд.Гос. УНЦ «Колледж» .2004.
185.
Иванов А. Н. Теоретическое
исследование гидродинамических характеристик крыльевых профилей при кавитации.
Материалы IX научно-технической конференции по теории корабля. Л.:”Судостроение
1968
186.
Иванов А.Н. Кавитационное
обтекание профилей крыльев . ИАН СССР . Серия механики и машиностроения 1960
Вып.6 С.117-119 .
187. Tulin
M. P. Supercavitating Flow pst Foils and
Struts . Symposium on Cavitation in Hydrodynamics .
188. Tulin
M. P. Supercavitating Flows . Small Perturbation Theory . J.S.R.1967 , Vol 7. №3.
189. Guerst
J. A. Linearized Theory for Partially Cavitating Hydrofoil . International
Shipbuilding Progress 1959 Vol 6. № 60
190. Wade
R.B. Linearized Theory for Partially Cavitating Plane -Conveх Hydrofoil Including the Effects of Comber and
Thickness. J. R. 1967 Vol. 11 №1.
191.
Терентьев А.Г. Плоские
стационарные задачи теории струйных и каитационных течений . Автореферат
докторской диссертации . Казань КГУ 1972.
192.
Косов Б.В. , Шалларь А. В.
Гидродинамические характеристики профилей крыльев в переходном режиме
кавитационного обтекания . Материалы по обмену опытом . Труды НТО СП
.Экспериментальная гидродинамика судна.Вып.226. .Л.”Судостроение“
193.
Басин М.А., Шалларь А.В.
Нестационарная схема обтекания кавитирующего крыла установившимся потоком. Труды НТО СП. Вып.192 .Л.”Судостроение“ 1973
194
Кнэпп.Р. Дейли Дж.,Хэммит Ф. Кавитация .
М.: “Мир” 1974.
195.
Ильин В. П. Структура и
шумообразование при пленочной кавитации. Всесоюзный симпозиум по проблемам
кавитации. Одесса .1971.
196.
Левковский Ю.Л. Структура
кавитационных течений . Л.: Судостроение. 1978 224 cтр.
197. Walchner O. Profilmessungen bei
Kavitation-Hydromechanische Probleme des Schiffsantriebs. Hamburg 1932
198. Numachi F. Kraftmessungen an fier
Flugel -profilen bei Hohlsog Forschung auf dem Gebiete des Ingeneur wesens. Band 11, №6,
1940.
199.
Иванов А.Н. Гидродинамика
развитых кавитационных течений. Л.”Судостроение”1980 240 с.
200. Meijer
M.C. Some Experiments of partly Cavitating Hydrofoils . International
Schipbuilding Progress Vol 6. №60 Аugust
1958 .
201. Биркгоф Г. Сарантонелло Э.Струи, следы и каверны. М.: “Мир
“1964.
202
Чжен П. Отрывные течения М.: Мир
1972-1973. Тт.1-3.
203.
Гогиш Л.В. , Нейланд В.Я. ,
степанов Г.Ю. Теория двумерных отрывных течений . Гидромеханика (Итоги науки )
1975.тт7.8
204.
Нейланд В.Я. , Степанов Г.Ю. Ламинарные и турбылентные течения . В кн.:”
Современные проблемы теоретической и прикладной механики .” Киев : “Наукова
думка”1978.С.216-232
205.
Гогиш Л.В. , Степанов Г.Ю.
Турбулентные отрывные течения М.:”Наука“1979,367с
206.
Хёрмандер Л. Анализ линейных дифференцальных операторов с частными
производными. В четырёх томах. М.:Мир.1986.
207. Басин
М.А., Косов Б.В. Шалларь А. В. Способ уменьшения сопротивления и вибрации
крыльевого гидродинамического профиля .АС №477 879 от 29.03.75. Заявка №1938937
с приоритетом от 2.07.73
208.
Басин М.А. , Косов Б.В.
,Шалларь А.В. Крыло с системой управления кавитацией , А.С. № 524729 от
22.04.76. Заявка №2023987 с приоритетом от 12.05.74.
209.
Косов Б.В. , Шалларь А.В.
Крыльевое устройство судна на подводных крыльях .А.С. №1080348 от 15.11.83
Заявка №3505758 с приоритетом от 08.07.82.
210.
Фрост Р. Ручей, текущий к западу. Из девяти книг.(Перевод А.Сергеева.
М.:ИЛ.1963
211.
Карман Т. Сверхзвуковая аэродинамика. Принципы и приложения. М. Государственное
издательство иностранной литературы. 1948. 100с.
212.
Франкль Ф.И. Карпович Е.А. Газодинамика тонких тел. М.-Л.: ОГИЗ - Гостехиздат.
1948. 176с.
213.
Рахматуллин Х. А., Сагомонян А. Я., Бунимович А. И., Зверев И. Н. Газовая
динамика. М.: Высшая школа. 1965. 724 с.
214.
Ван Дайк М. Альбом течений жидкости и газа.М.: Мир. 1986. 184с.
215.
Басин А.М., Веледицкий И.О., Ляховицкий А. Г. Гидродинамика судов на
мелководье. Л.: Судостроение. 19
216.
Басин А. М. Судно наименьшего волнового сопротивления на мелководье.Труды ЛКИ.
1940 Вып.V.
217.
Басин А. М. Исследование движения судна в канале. Труды ЦНИИРФ, 1956. Вып.XXIII.
218.
Басин А. М. Приближёное исследование волнового сопротивления судна, движущегося
со сверхкритическими скоростями. Труды ЦНИИРФ, Л.: 1959. Вып.XXXIX.
219.
Басин А. М. О форме судна наименьшего сопротивления , движущегося со
сверхкритическими скоростями. Труды ЛИВТ. 1962 Вып. 33.
220.
Басин А. М. Тонкие суда наименьшего сопротивления , движущиеся со
сверхкритическими скоростями. Труды ЛИВТ. 1974. Вып. 147.
221.
Басин А. М., Веледницкий И. О., Ляховицкий А. Г., Степанюк Е. И.
Сверхкритические режимы движения судов на мелководье. Сборник «Сопротивление воды движению судов»,
Материалы по обмену опытом. НТО СП им акад. А.Н. Крылова. Л.: «Судостроение»
1969. Вып.127.
222.
Басин А.М. Ляховицкий А.Г. Со сверхкритической скоростью «Водный транспорт»
1969. № 135 (5574)
223.
Басин А.М., Ляховицкий А. Г. Особенности гидродинамики мелкосидящих судов со
сверхкритическими скоростями. «Речной транспорт» 1972. № 12.
224.
Басин А.М., Ляховицкий А. Г. Перспективы развития быстроходных водоизмещающих
судов. «Речной транспорт» 1972. № 6.
225. Басин А.М., Ляховицкий А. Г. Речные
водоизмещающие суда со сверхкритическими скоростями. «Судостроение» 1972. № 7.
226.
Веледницкий И.О., Ляховицкий А.Г. Влияние характеристик теоретического чертежа
на остаточное сопротивление быстроходных водоизмещающих судов в условиях
мелководья. Труды ЛИВТ. 1968.
227.
Веледницкий И.О., Ляховицкий А.Г., Степанюк Е.И. Некоторые вопросы ходкости и
мореходности судов со сверхкритическими скоростями хода. Теория корабля.
Материалы к XXIII научно-технической
конференции ЛИВТ . 1969.
228
Ляховицкий А. Г. Сравнительная оценка сопротивления воды движению однокорпусных
и двухкорпусных судов со сверхкритическими скоростями. Труды ЛИВТ. 1972. Вып. 133.
229.Basin M.A. The Influence of Froude Number
Calculated by Displacement on the Form of the Hydrodynamic Complex of Surface
Ships. II Symposium on High Speed Marine Vehicles.
230.Basin M.A., Lordkipanidze A,N., Mizina M.
Ja., Zelensky B.M., Waldman V. A. Computer Technology for Design of
Hydrodynamic Complex of Dynamically Supported
Crafts. Proceedings of the VI
Congress of the IMAM. Edited by Peter A. Bogdanov, Vol III. 15-20
Nnovember 1993.
231. Basin M. A., Ljakhovitsky A. G., Shur
S.B., Zelensky B.M. The Methods of
Determining of Fast Catamarans Hydrodynamic Complex Characteristics. IMAM Proceedings of the VII
Congress. Edited by Vladimir Androchec and Josip Lovrich. Dubrovnic.
232. Basin M. A., Ljakhovitsky A. G., Shur
S.B., Zelensky B. M. Hydrodynamics of Fast Catamarns. Proceedings of Fast 95.
Berlin-Hamburg. August-September 1995. P.57-67.
233. Шмидт – Ниельсен К. Размеры животных. Почему они так важны? М.:
Мир.1987.
